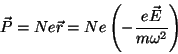Next: A energia do campo
Up: dispersion
Previous: Equações constitutivas
No limite
 não há polarização, ou
seja,
não há polarização, ou
seja,
 . A seguir obteremos o
comportamento de
. A seguir obteremos o
comportamento de
 para grandes valores de
para grandes valores de  de forma mais detalhada usando um modelo muito simples.
de forma mais detalhada usando um modelo muito simples.
Se a freqüência for grande comparada às freqüências dos
movimentos de todos os elétrons, esses poderão ser considerados
livres. Além disso, de 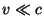 segue que
segue que
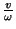 ,
a distância percorrida por um elétron durante um período da
oscilação satisfaz a
,
a distância percorrida por um elétron durante um período da
oscilação satisfaz a
Logo, o elétron, durante um período, explora uma
pequeniníssima porção de um comprimento de onda, ou seja,
praticamente não sente a variação espacial do campo. Pode-se,
então, tomar o campo como uniforme. A equação de movimento do
elétron será
ou
pois, para a dependência harmônica 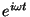 da velocidade,
a derivada no tempo é equivalente à multiplicação por
da velocidade,
a derivada no tempo é equivalente à multiplicação por
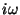 . Logo,
. Logo,
e, também,
O vetor de polarização 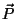 (momento de dipolo induzido por
unidade de volume) é
(momento de dipolo induzido por
unidade de volume) é
onde 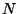 é o número de elétrons por unidade de volume.
Conseqüentemente,
é o número de elétrons por unidade de volume.
Conseqüentemente,
A relação bem conhecida (que é, de fato, a definição de
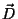 )
)
leva então a
ou, finalmente, a
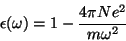 |
(10) |
que é o limite procurado.



Next: A energia do campo
Up: dispersion
Previous: Equações constitutivas
Henrique Fleming
2003-03-21
![]() segue que
segue que
![]() ,
a distância percorrida por um elétron durante um período da
oscilação satisfaz a
,
a distância percorrida por um elétron durante um período da
oscilação satisfaz a