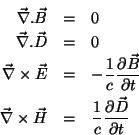Next: Limite de altas freqüências
Up: dispersion
Previous: Introdução
As equações de Maxwell
e a expressão da polarização,
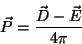 |
(1) |
precisam ser suplementadas por equações constitutivas. Para
freqüências altas temos, normalmente, campos fracos, o que sugere
uma relação linear entre 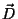 e
e 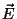 . A existência
de memória sugere, então,
. A existência
de memória sugere, então,
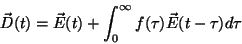 |
(2) |
Introduzindo as transformadas de Fourier
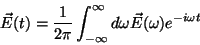 |
(3) |
obtém-se1
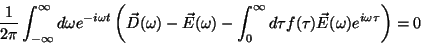 |
(4) |
ou seja,
Portanto, para campos periódicos, é vantajoso expressar as equções
constitutivas em termos da freqüência; naturalmente
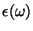 depende das propriedades do meio.
Note que
depende das propriedades do meio.
Note que
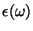 é um número complexo, podendo ser
escrito
é um número complexo, podendo ser
escrito
e, usando Eq.(![[*]](/usr/share/latex2html/icons/crossref.png) ),
),
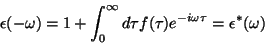 |
(7) |
Equivalentes à relação
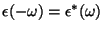 são:
são:
ou seja, a parte real de 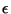 é uma função par; a parte
imaginária é uma função ímpar. Numa expansão em
série de potências de
é uma função par; a parte
imaginária é uma função ímpar. Numa expansão em
série de potências de 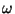 , a parte real de
, a parte real de 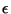 começará com uma potência zero de
começará com uma potência zero de 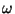 (a constante
dielétrica ordinária), vindo a seguir uma correção
quadrática. Já a parte imaginária conterá apenas potências
ímpares, e, em particular, se anula para
(a constante
dielétrica ordinária), vindo a seguir uma correção
quadrática. Já a parte imaginária conterá apenas potências
ímpares, e, em particular, se anula para 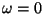 . Em outras
palavras, o limite da eletrostática não oferece qualquer
informação sobre a parte imaginária da permissividade (que é
o nome ``oficial'' de
. Em outras
palavras, o limite da eletrostática não oferece qualquer
informação sobre a parte imaginária da permissividade (que é
o nome ``oficial'' de 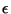 ).
).



Next: Limite de altas freqüências
Up: dispersion
Previous: Introdução
Henrique Fleming
2003-03-21