


Next: Retomando a estrada
Up: O dipolo magnético
Previous: Exibindo o dipolo magnético
O seguinte teorema, corolário do teorema de Stokes, facilitará muito
a nossa tarefa:
Seja 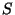 uma superfície delimitada por uma curva fechada
com um sentido de percurso escolhido. Seja
uma superfície delimitada por uma curva fechada
com um sentido de percurso escolhido. Seja 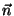 o campo das normais
à superfície, coordenadas com o sentido de percurso pela ``regra do
saca-rolhas''. Seja ainda
o campo das normais
à superfície, coordenadas com o sentido de percurso pela ``regra do
saca-rolhas''. Seja ainda 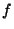 uma função. Então,
uma função. Então,
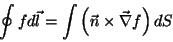 |
(17) |
A demonstração é uma aplicação direta do teorema de Stokes. Considere
o campo vetorial 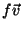 , onde
, onde 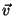 é um campo constante (uniforme,
na linguagem dos físicos). Pelo teorema de Stokes, temos
é um campo constante (uniforme,
na linguagem dos físicos). Pelo teorema de Stokes, temos
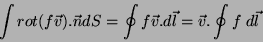 |
(18) |
Mas
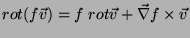 ,e,
como
,e,
como 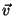 é constante,
é constante, 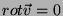 . Logo,
. Logo,
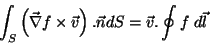 |
(19) |
Mas
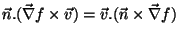 , logo,
, logo,
Para que isto seja verdade para qualquer 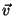 constante,
devemos ter a Eq.(17) satisfeita.
constante,
devemos ter a Eq.(17) satisfeita.
Henrique Fleming
2002-04-20
![]() uma superfície delimitada por uma curva fechada
com um sentido de percurso escolhido. Seja
uma superfície delimitada por uma curva fechada
com um sentido de percurso escolhido. Seja ![]() o campo das normais
à superfície, coordenadas com o sentido de percurso pela ``regra do
saca-rolhas''. Seja ainda
o campo das normais
à superfície, coordenadas com o sentido de percurso pela ``regra do
saca-rolhas''. Seja ainda ![]() uma função. Então,
uma função. Então,