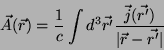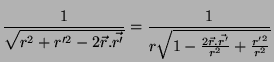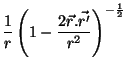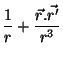Next: Um teorema útil
Up: O dipolo magnético
Previous: O potencial vetor
Uma distribuição de correntes estacionárias é descrita
por um campo vetorial
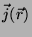 que é tal que
que é tal que
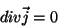 |
(6) |
O potencial vetor gerado por essa distribuição é
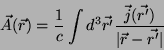 |
(7) |
As correntes estão confinadas numa região finita, ou seja,
existe um valor 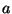 tal que
tal que
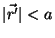 . Estamos observando
essa distribuição de longe, ou seja,
. Estamos observando
essa distribuição de longe, ou seja, 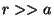 . Neste caso,
. Neste caso,
desprezando-se os termos adicionais, que são pequenos. Logo,
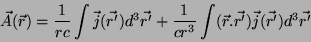 |
(11) |
A primeira integral se anula para correntes estacionárias. De fato,
sendo 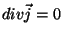 , temos
, temos
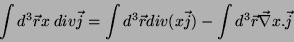 |
(12) |
ou
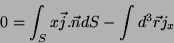 |
(13) |
onde usamos o teorema do divergente para transformar a primeira integral
do segundo membro da Eq.(12) em uma integral de superfície.
Como a integração era sobre todo o volume, a superfície está no infinito,
onde o integrando é zero, como toda quantidade física. Por isso, na
Eq.(13), a primeira integral do segundo membro é nula, e se
obtém
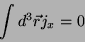 |
(14) |
De forma análoga se mostra que as demais componentes também se anulam,
e, portanto,
que
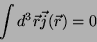 |
(15) |
se 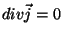 .
Temos, assim, para uma distribuição estacionária de correntes ``olhada
de longe'',
.
Temos, assim, para uma distribuição estacionária de correntes ``olhada
de longe'',
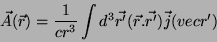 |
(16) |



Next: Um teorema útil
Up: O dipolo magnético
Previous: O potencial vetor
Henrique Fleming
2002-04-20