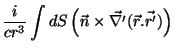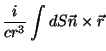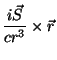Next: About this document ...
Up: O dipolo magnético
Previous: Um teorema útil
Tínhamos obtido que
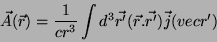 |
(20) |
Para circuitos em fios.
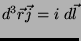 , logo,
, logo,
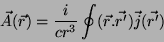 |
(21) |
Usando o nosso teorema, temos
onde usamos que
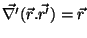 . Além
disso, supusemos que o circuito é uma curva plana, e que
a superfície de integração é um trecho do plano. neste caso,
. Além
disso, supusemos que o circuito é uma curva plana, e que
a superfície de integração é um trecho do plano. neste caso,
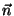 é um vetor constante, e
é um vetor constante, e
onde a última igualdade define o ``vetor superfície'', 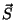 ,
que é um vetor cujo módulo é a área da superfície,
perpendicular à superfície e com o sentido coordenado ao sentido
de percurso da curva pela regra do saca-rolhas. Resumindo, temos
,
que é um vetor cujo módulo é a área da superfície,
perpendicular à superfície e com o sentido coordenado ao sentido
de percurso da curva pela regra do saca-rolhas. Resumindo, temos
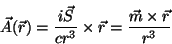 |
(25) |
com
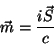 |
(26) |
Assim, descobrimos que o momento de dipolo magnético de
um circuito simples (anel de corrente) é proporcional
à sua área e à corrente que passa pelo fio.



Next: About this document ...
Up: O dipolo magnético
Previous: Um teorema útil
Henrique Fleming
2002-04-20