


Next: Coordenadas esféricas
Up: Meio
Previous: Meio
A eq.(9) será usada para obter a propriedade
fundamental do gradiente. Podemos escrevê-la
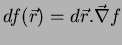 |
(11) |
que é lida assim: quando o argumento de 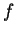 (nome bonito para
(nome bonito para
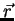 ) é alterado pelo vetor
) é alterado pelo vetor 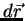 , ou seja, passa de
, ou seja, passa de
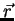 para
para
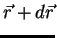 , a função varia de
, a função varia de 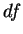 .
Em (11), tomemos
.
Em (11), tomemos
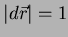 , o que dá, para
o módulo de
, o que dá, para
o módulo de 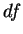 :
:
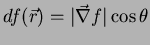 |
(12) |
onde 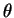 é o ângulo entre os vetores
é o ângulo entre os vetores 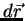 e
e
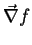 . De (12) vemos que, dado
. De (12) vemos que, dado
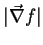 ,
o máximo acréscimo à função
,
o máximo acréscimo à função 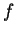 se dá para aquela
direção de
se dá para aquela
direção de 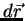 que corresponde ao máximo valor de
que corresponde ao máximo valor de
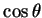 , ou seja,
, ou seja, 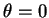 . Isto é, o máximo acréscimo
de
. Isto é, o máximo acréscimo
de 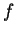 ocorre quando
ocorre quando 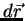 tem a mesma direção (e sentido)
que o vetor
tem a mesma direção (e sentido)
que o vetor
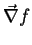 . Em palavras, o gradiente de uma
função aponta para a direção de máximo crescimento dessa
função.
. Em palavras, o gradiente de uma
função aponta para a direção de máximo crescimento dessa
função.
Henrique Fleming
2003-08-11