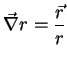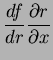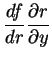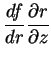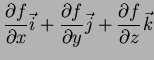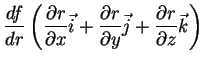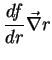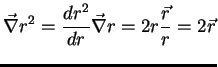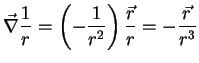Next: Meio
Up: Diferenciabilidade for the practical
Previous: Diferenciabilidade for the practical
Suponho que o leitor destas notas esteja familiarizado com
funções de uma variável real, e de valores reais, que
sejam contínuas e diferenciáveis até qualquer ordem.
Estas funções têm o nome de funções
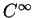 . Os físicos se referem a elas dizendo que são
bem comportadas.
. Os físicos se referem a elas dizendo que são
bem comportadas.
Para um tratamento semelhante ao meu, mas com figuras bonitas, veja
http://oregonstate.edu/dept/math/CalculusQuestStudyGuides/vcalc/partial/partial.html
Para funções diferenciáveis de uma variável, temos uma maneira
importantíssima de resolver o seguinte problema: dado o valor da função
em um ponto  , determinar o valor dela num outro ponto, bem próximo,
, determinar o valor dela num outro ponto, bem próximo, .
Seja
.
Seja 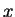 a coordenada do ponto
a coordenada do ponto  , e
, e 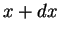 a coordenada do ponto
a coordenada do ponto  . Então
. Então
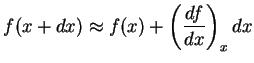 |
(1) |
que é a fórmula dos acréscimos finitos.
Exercícios:
(1)Mostre que, para 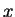 muito pequeno,
muito pequeno,
(2)A correção seguinte é dada pela fórmula
 |
(2) |
Para cada função do exercício (1), calcule esta nova
aproximação.
Consideremos agora uma função de 3 variáveis,
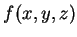 com valores reais. Os matemáticos diriam:
com valores reais. Os matemáticos diriam:
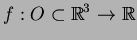 |
(3) |
onde 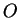 é um aberto de
é um aberto de
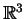 . Gostaríamos de ter
uma fórmula dos acréscimos finitos também neste caso. Para
isso precisamos do conceito de derivada parcial. Uma função
como a que descrevemos será diferenciável se existirem, e forem
contínuas, as funções
. Gostaríamos de ter
uma fórmula dos acréscimos finitos também neste caso. Para
isso precisamos do conceito de derivada parcial. Uma função
como a que descrevemos será diferenciável se existirem, e forem
contínuas, as funções
 ,
,
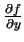 ,
,
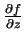 ,
denominadas derivadas parciais de
,
denominadas derivadas parciais de 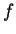 , e definidas assim:
, e definidas assim:
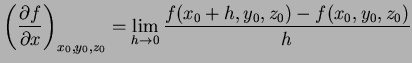 |
(4) |
ou seja, é a derivada de 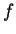 em relação a
em relação a 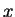 como se
como se
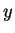 e
e 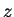 fossem constantes. Definições análogas são
dadas para
fossem constantes. Definições análogas são
dadas para
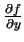 e
e
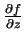 .
.
Um ponto de coordenadas
 pode ser representado
pelo vetor
pode ser representado
pelo vetor
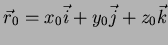 .
Um ponto genérico é representado pelo vetor
.
Um ponto genérico é representado pelo vetor
 . Um valor genérico da
função
. Um valor genérico da
função 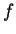 pode então ser escrito como
pode então ser escrito como
 |
(5) |
Diz-se que uma função 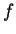 é contínua no ponto
é contínua no ponto
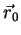 se, dado
se, dado
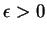 , existe
, existe 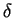 tal que
tal que
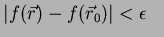 desde que desde que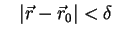 |
(6) |
Em palavras, para 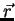 muito próximo de
muito próximo de
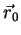 ,
,
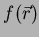 é muito próximo de
é muito próximo de
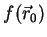 . Uma função
é diferenciável se: (1) For contínua; (2) Seu gráfico não
tiver ``bicos'' ou ``vincos''. No caso de uma função de duas
variáveis,
. Uma função
é diferenciável se: (1) For contínua; (2) Seu gráfico não
tiver ``bicos'' ou ``vincos''. No caso de uma função de duas
variáveis, 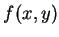 , podemos visualizar esse conceito assim: o
gráfico da função, ou seja, o gráfico
, podemos visualizar esse conceito assim: o
gráfico da função, ou seja, o gráfico  , é, se
ela for contínua, uma superfície ``acima'' do plano
, é, se
ela for contínua, uma superfície ``acima'' do plano 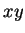 .
A função é diferenciável num ponto
.
A função é diferenciável num ponto 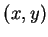 , se o a
superfície do gráfico tiver um plano tangente no ponto
, se o a
superfície do gráfico tiver um plano tangente no ponto
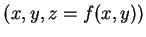 . Neste caso, localmente, a superfície do
gráfico se confunde com o plano tangente. Veja as figuras da segunda
referência da internet, abaixo.
. Neste caso, localmente, a superfície do
gráfico se confunde com o plano tangente. Veja as figuras da segunda
referência da internet, abaixo.
A fórmula dos acréscimos finitos, neste caso, é
 |
(7) |
sendo as derivadas parciais do segundo membro calculadas no ponto
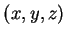 .
.
Exemplos:
(1)
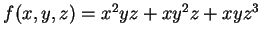 .
.
As derivadas parciais são:
(2)
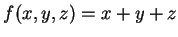
(3)

(4) Resultados importantes:
Exercícios:
(1) Considere a função
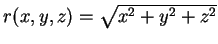
(a)Calcule as derivadas parciais
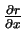 ,
,
 e
e
 .
.
(b)Usando a fórmula dos acréscimos finitos, calcule
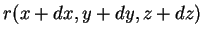 .
.
(c) Seja
 Mostre que
Mostre que
A fórmula dos acréscimos finitos, eq.(7), pode ser
reescrita em termos de vetores: seja
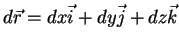 . Defino
o gradiente de
. Defino
o gradiente de 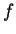 assim:
assim:
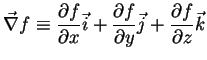 |
(8) |
O símbolo
 é pronunciado ``nabla'' porque,
diz-se, tem a forma de uma antigo instrumento musical hebraico. Outros
dizem que é a letra ``G'' no alfabeto Klingon. Go figure!
é pronunciado ``nabla'' porque,
diz-se, tem a forma de uma antigo instrumento musical hebraico. Outros
dizem que é a letra ``G'' no alfabeto Klingon. Go figure!
O fato é que a fórmula dos acréscimos finitos pode agora ser
escrita assim:
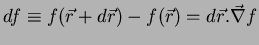 |
(9) |
Exemplos:
(1)A função
 é a distância
do ponto de coordenadas
é a distância
do ponto de coordenadas 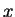 ,
, 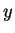 e
e 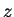 à origem. Calculemos
o seu gradiente. Verifica-se facilmente que
à origem. Calculemos
o seu gradiente. Verifica-se facilmente que
Logo, temos
e, como
 , o resultado é
Notando que
, o resultado é
Notando que 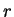 é o módulo de
é o módulo de 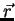 , vemos que o gradiente
de
, vemos que o gradiente
de 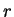 é o vetor unitário na direção radial, ou seja, na
direção em que a distância do ponto
é o vetor unitário na direção radial, ou seja, na
direção em que a distância do ponto 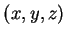 à origem cresce
mais rapidamente. Veremos que isto não é coincidência.
à origem cresce
mais rapidamente. Veremos que isto não é coincidência.
(2) Considere uma função qualquer da variável 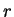 ,
que vem a ser a função descrita acima. Temos aqui um
caso de função composta (ou ``função de função''):
e a função é, em última análise, função de
,
que vem a ser a função descrita acima. Temos aqui um
caso de função composta (ou ``função de função''):
e a função é, em última análise, função de
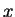 ,
, 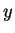 e
e 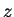 . Temos, então, de calcular derivadas
. Temos, então, de calcular derivadas
 , etc. Demonstra-se o importante resultado, denominado
regra da cadeia:1
, etc. Demonstra-se o importante resultado, denominado
regra da cadeia:1
Podemos agora calcular
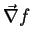 :
:
Obtivemos, assim, uma fórmula muito importante:
 |
(10) |
Exemplos:



Next: Meio
Up: Diferenciabilidade for the practical
Previous: Diferenciabilidade for the practical
Henrique Fleming
2003-08-11
![]() , determinar o valor dela num outro ponto, bem próximo,
, determinar o valor dela num outro ponto, bem próximo,![]() .
Seja
.
Seja ![]() a coordenada do ponto
a coordenada do ponto ![]() , e
, e ![]() a coordenada do ponto
a coordenada do ponto ![]() . Então
. Então
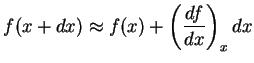

![]() com valores reais. Os matemáticos diriam:
com valores reais. Os matemáticos diriam:
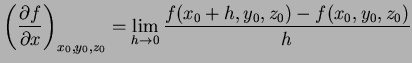
![]() pode ser representado
pelo vetor
pode ser representado
pelo vetor
![]() .
Um ponto genérico é representado pelo vetor
.
Um ponto genérico é representado pelo vetor
![]() . Um valor genérico da
função
. Um valor genérico da
função ![]() pode então ser escrito como
pode então ser escrito como
![]()
![]() ,
,
![]() e
e
![]() .
.
![]() .
.
![]() Mostre que
Mostre que
![]() . Defino
o gradiente de
. Defino
o gradiente de ![]() assim:
assim:
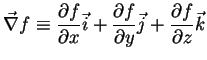
![]() é a distância
do ponto de coordenadas
é a distância
do ponto de coordenadas ![]() ,
, ![]() e
e ![]() à origem. Calculemos
o seu gradiente. Verifica-se facilmente que
à origem. Calculemos
o seu gradiente. Verifica-se facilmente que