


Next: Teorema do divergente
Up: Campos vetoriais for the
Previous: Comentários
Na eletrostática temos as equações básicas
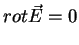 |
(165) |
(que significa que a força eletrostática é conservativa)
e, nas regiões onde não há cargas,
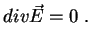 |
(166) |
A primeira dessas equações é equivalente a
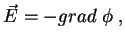 |
(167) |
onde 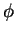 é o potencial escalar. Usando 167 em
166, temos
é o potencial escalar. Usando 167 em
166, temos
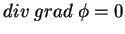 |
(168) |
ou
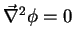 |
(169) |
onde
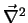 é o operador Laplaceano. A equação
169 é a famosa equação de Laplace. Boa parte
de sua fama é devida a um poderoso teorema de existência
e unicidade que é o tema principal dessas notas. Para demonstrar
esse teorema precisamos do teorema do divergente.
é o operador Laplaceano. A equação
169 é a famosa equação de Laplace. Boa parte
de sua fama é devida a um poderoso teorema de existência
e unicidade que é o tema principal dessas notas. Para demonstrar
esse teorema precisamos do teorema do divergente.
Numa região onde há cargas, não vale a equação de Laplace,
que é substituída pela equação de Poisson,
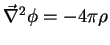 |
(170) |
onde 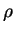 é a densidade volumétrica de carga. Por outro lado,
generalizando a lei de Coulomb, vimos que
é a densidade volumétrica de carga. Por outro lado,
generalizando a lei de Coulomb, vimos que
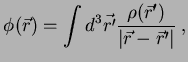 |
(171) |
e que, portanto, a Eq.(171) exibe uma solução da
Eq.(170). De fato, (171) é a solução
de (170) que se anula no infinito. Mais tarde vamos
estudar o método inventado por George Green para obter este
resultado trabalhando diretamente com a equação de Poisson.
Subsections



Next: Teorema do divergente
Up: Campos vetoriais for the
Previous: Comentários
Henrique Fleming
2003-08-11