


Next: Máximos e mínimos
Up: A magia da equação
Previous: Fórmulas de Green
O grande poder da equação de Laplace está no fato de que, em certas condições,
pode-se garantir a existência e a unicidade da solução. Assim, qualquer
que seja o método pelo qual a solução é obtida, a solução é aquela,
e nenhuma outra. Vamos demonstrar aqui a unicidade. O teorema de existência
é difícil, e sua demonstração ajuda pouco na compreensão do
problema.
Suponhamos que 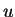 seja harmônica no volume
seja harmônica no volume 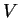 , e tomemos
, e tomemos 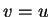 .
Usando a Eq.(177) temos então
.
Usando a Eq.(177) temos então
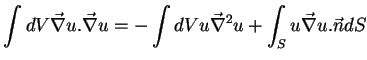 |
(180) |
Logo,
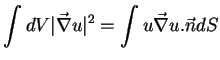 |
(181) |
Uma conseqüência dessa fórmula é a seguinte: seja 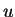 harmônica
em
harmônica
em 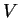 e nula em
e nula em 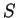 , que é a superfície que delimita
, que é a superfície que delimita 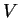 . Então
. Então
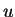 é nula em
é nula em 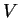 . De fato,
. De fato,
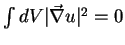 implica em
implica em
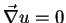 em
em 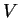 , e, portanto,
, e, portanto,
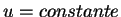 em
em
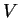 . Como
. Como 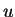 é contínua, esta constante tem de ser zero, pois
é contínua, esta constante tem de ser zero, pois
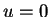 na superfície.
na superfície.
Sejam agora 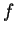 e
e 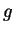 duas funções harmônicas em
duas funções harmônicas em 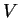 e tais que
e tais que
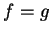 na superfície que delimita este volume. Então,
na superfície que delimita este volume. Então, 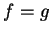 em
todo o volume. De fato, basta aplicar o teorema anterior para
a função
em
todo o volume. De fato, basta aplicar o teorema anterior para
a função 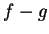 .
.
Chegamos assim ao enunciado do grande teorema de unicidade: se
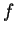 é uma solução da equação de Laplace que tem valores determinados
sobre uma superfície fechada,
é uma solução da equação de Laplace que tem valores determinados
sobre uma superfície fechada, 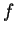 é única. Um exemplo de
aplicação deste teorema com relevância para a física é o
seguinte: determinar uma função que satisfaça a equação de
Laplace no interior de uma superfície fechada e que seja
constante, igual a
é única. Um exemplo de
aplicação deste teorema com relevância para a física é o
seguinte: determinar uma função que satisfaça a equação de
Laplace no interior de uma superfície fechada e que seja
constante, igual a 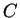 , nessa superfície. Seja
, nessa superfície. Seja 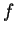 a função
constante cujo valor é
a função
constante cujo valor é 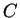 . Ela é solução da equação de
Laplace, e seu valor sobre a superfície fechada é
. Ela é solução da equação de
Laplace, e seu valor sobre a superfície fechada é 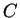 . Logo,
pelo teorema de unicidade, esta função é a única função
que satisfaz a equação de Laplace e vale
. Logo,
pelo teorema de unicidade, esta função é a única função
que satisfaz a equação de Laplace e vale 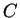 na superfície
considerada. Na física, o potencial eletrostático, em uma
região onde não há cargas, é harmônico (satisfaz a
equação de Laplace). Por outro lado, sabe-se que, no equilíbrio,
o potencial sobre a superfície de um condutor é constante. Logo,
como, dentro de um condutor, a carga é zero, temos que o potencial
é constante, com aquele valor que ele assume na superfície.
Segue como conseqüência que o campo elétrico é zero, no interior
do condutor.
na superfície
considerada. Na física, o potencial eletrostático, em uma
região onde não há cargas, é harmônico (satisfaz a
equação de Laplace). Por outro lado, sabe-se que, no equilíbrio,
o potencial sobre a superfície de um condutor é constante. Logo,
como, dentro de um condutor, a carga é zero, temos que o potencial
é constante, com aquele valor que ele assume na superfície.
Segue como conseqüência que o campo elétrico é zero, no interior
do condutor.



Next: Máximos e mínimos
Up: A magia da equação
Previous: Fórmulas de Green
Henrique Fleming
2003-08-11
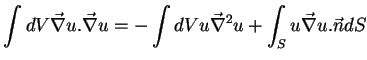
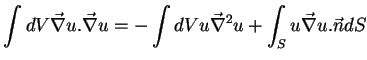
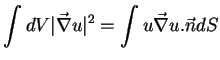
![]() e
e ![]() duas funções harmônicas em
duas funções harmônicas em ![]() e tais que
e tais que
![]() na superfície que delimita este volume. Então,
na superfície que delimita este volume. Então, ![]() em
todo o volume. De fato, basta aplicar o teorema anterior para
a função
em
todo o volume. De fato, basta aplicar o teorema anterior para
a função ![]() .
.
![]() é uma solução da equação de Laplace que tem valores determinados
sobre uma superfície fechada,
é uma solução da equação de Laplace que tem valores determinados
sobre uma superfície fechada, ![]() é única. Um exemplo de
aplicação deste teorema com relevância para a física é o
seguinte: determinar uma função que satisfaça a equação de
Laplace no interior de uma superfície fechada e que seja
constante, igual a
é única. Um exemplo de
aplicação deste teorema com relevância para a física é o
seguinte: determinar uma função que satisfaça a equação de
Laplace no interior de uma superfície fechada e que seja
constante, igual a ![]() , nessa superfície. Seja
, nessa superfície. Seja ![]() a função
constante cujo valor é
a função
constante cujo valor é ![]() . Ela é solução da equação de
Laplace, e seu valor sobre a superfície fechada é
. Ela é solução da equação de
Laplace, e seu valor sobre a superfície fechada é ![]() . Logo,
pelo teorema de unicidade, esta função é a única função
que satisfaz a equação de Laplace e vale
. Logo,
pelo teorema de unicidade, esta função é a única função
que satisfaz a equação de Laplace e vale ![]() na superfície
considerada. Na física, o potencial eletrostático, em uma
região onde não há cargas, é harmônico (satisfaz a
equação de Laplace). Por outro lado, sabe-se que, no equilíbrio,
o potencial sobre a superfície de um condutor é constante. Logo,
como, dentro de um condutor, a carga é zero, temos que o potencial
é constante, com aquele valor que ele assume na superfície.
Segue como conseqüência que o campo elétrico é zero, no interior
do condutor.
na superfície
considerada. Na física, o potencial eletrostático, em uma
região onde não há cargas, é harmônico (satisfaz a
equação de Laplace). Por outro lado, sabe-se que, no equilíbrio,
o potencial sobre a superfície de um condutor é constante. Logo,
como, dentro de um condutor, a carga é zero, temos que o potencial
é constante, com aquele valor que ele assume na superfície.
Segue como conseqüência que o campo elétrico é zero, no interior
do condutor.