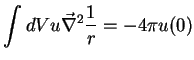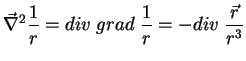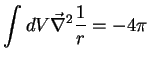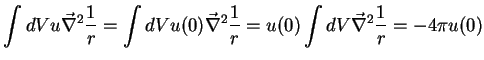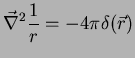Next: Apêndice: Two theorems by
Up: A magia da equação
Previous: Aplicações
A equação
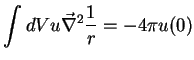 |
(194) |
merece tratamento especial. Em primeiro lugar, porque uma cálculo
apressado de
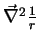 dá zero, o que daria
zero para o primeiro membro. Mas esse cálculo está errado, pois
a função
dá zero, o que daria
zero para o primeiro membro. Mas esse cálculo está errado, pois
a função
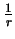 é descontínua no ponto
é descontínua no ponto 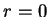 . Uma maneira
de descobrir que o laplaceano de
. Uma maneira
de descobrir que o laplaceano de
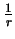 não é sempre
zero é pelo uso do teorema do divergente. De fato,
logo, tomando uma esfera de raio
não é sempre
zero é pelo uso do teorema do divergente. De fato,
logo, tomando uma esfera de raio 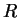
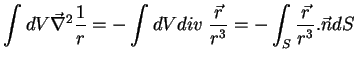 |
(195) |
e isto é o fluxo do campo elétrico
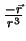 ,
que é o campo de uma carga -1 colocada na origem. Logo, pelo
teorema de Gauss, esse fluxo é igual a
,
que é o campo de uma carga -1 colocada na origem. Logo, pelo
teorema de Gauss, esse fluxo é igual a 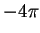 . Conseqüentemente,
o primeiro membro da Eq.(195) não pode ser zero,
ou seja,
. Conseqüentemente,
o primeiro membro da Eq.(195) não pode ser zero,
ou seja,
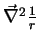 não pode ser identicamente
zero. No entanto, para
não pode ser identicamente
zero. No entanto, para 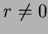 , o laplaceano é nulo, pois
a função é contínua, e o cálculo direto está correto. Logo,
é no ponto
, o laplaceano é nulo, pois
a função é contínua, e o cálculo direto está correto. Logo,
é no ponto 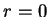 que acontece alguma coisa interessante.
Incidentalmente, mostramos que
que acontece alguma coisa interessante.
Incidentalmente, mostramos que
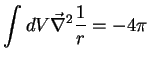 |
(196) |
Voltemos ao cálculo da Eq.(194). Note-se que, para
qualquer 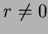 ,
,
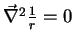 , ou seja,
o valor da função
, ou seja,
o valor da função 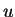 para
para 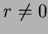 é irrelevante para
o cálculo da integral, uma vez que vem sempre multiplicado
por 0. O único valor de
é irrelevante para
o cálculo da integral, uma vez que vem sempre multiplicado
por 0. O único valor de 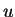 que interessa é
que interessa é 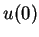 . Logo,
a integral não se altera se substituirmos
. Logo,
a integral não se altera se substituirmos 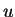 pela função
constante que tem o valor
pela função
constante que tem o valor 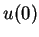 em todos os pontos. Assim,
em todos os pontos. Assim,
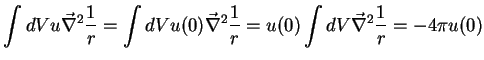 |
(197) |
que é o resultado que queríamos obter.
Em tratamentos mais avançados se demonstra a seguinte relação:
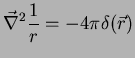 |
(198) |
onde, no segundo membro, aparece a ``função'' delta de Dirac. Este
resultado sintetiza o resultado anterior e muitos outros
semelhantes. Veja, por exemplo, as minhas notas sobre as funções
de Green, e sobretudo, a grande obra de Dirac [5],
``Principles of Quantum Mechanics'', tida por muitos como o maior livro de
Física desde os ``Principia'' de Newton[6].



Next: Apêndice: Two theorems by
Up: A magia da equação
Previous: Aplicações
Henrique Fleming
2003-08-11