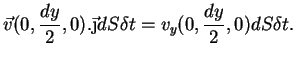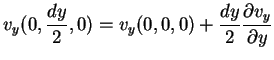Next: O teorema de Helmholtz
Up: Campos vetoriais for the
Previous: O rotacional
O teorema do divergente, ou de Gauss, é o
instrumento matemático que melhor permite visualizar que tipos
de campos vetoriais possuem divergente não-nulo. Vamos
enunciá-lo num contexto concreto. O problema é o seguinte:
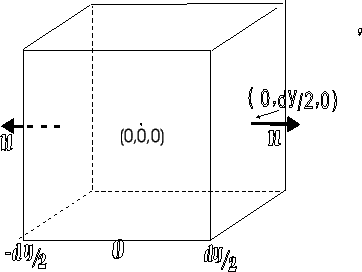
a figura abaixo representa uma região cúbica do espaço por onde
flui uma corrente de água. Trata-se de um cubo geométrico, sem
existência física: uma porção do espaço. Queremos calcular quanta
água sai do cubo
num intervalo de tempo 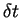 , ou, mais precisamente, a
diferença entre a quantidade de água que sai e a que entra.
Naturalmente, supõe-se que a
única maneira de a água sair do cubo, ou entrar nele, é atravessando uma de
suas faces.
Os eixos coordenados são escolhidos de maneira que sejam
perpendiculares às faces. O centro do cubo é o ponto de
coordenadas (
, ou, mais precisamente, a
diferença entre a quantidade de água que sai e a que entra.
Naturalmente, supõe-se que a
única maneira de a água sair do cubo, ou entrar nele, é atravessando uma de
suas faces.
Os eixos coordenados são escolhidos de maneira que sejam
perpendiculares às faces. O centro do cubo é o ponto de
coordenadas (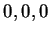 ). Assim, os vetores
). Assim, os vetores 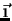 ,
,
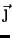 ,
,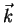 , são vetores unitários normais, cada um a
um par de faces. Tomemos, em cada face, a normal externa.
Então, por exemplo, na face em
, são vetores unitários normais, cada um a
um par de faces. Tomemos, em cada face, a normal externa.
Então, por exemplo, na face em 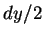 , a normal externa
, a normal externa
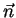 será
será 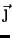 , ao passo que, na face em
, ao passo que, na face em 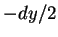 ,
,
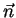 será
será 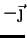 .
.
Suponhamos que as faces do cubo sejam suficientemente pequenas
para que o valor da velocidade da água nos vários pontos de
uma face possam ser considerados iguais. (Se não for, diminua-se
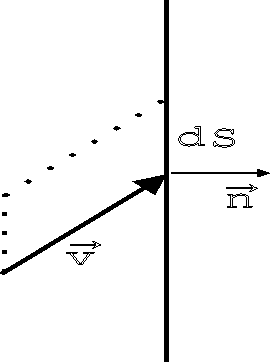
o cubo!). Na figura abaixo vemos como calcular a quantidade de
água que atravessa uma face, no tempo 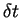 .
.
A quantidade
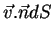 |
(99) |
é o volume da região tracejada. Na unidade de tempo, toda a
água que estiver aí dentro atravessará 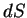 , e nenhuma
outra. Então, se
, e nenhuma
outra. Então, se 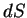 for a superfície de uma face do cubo
e
for a superfície de uma face do cubo
e 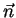 for a normal externa. no intervalo de tempo
for a normal externa. no intervalo de tempo 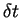 , um volume de água dado por
, um volume de água dado por
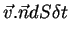 |
(100) |
atravessará essa face. Consideremos a face localizada em 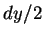 .
O volume de água que atravessará a face é
.
O volume de água que atravessará a face é
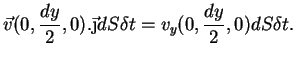 |
(101) |
Como 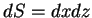 , isto é igual a
, isto é igual a
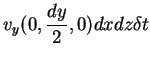 |
(102) |
Usando a fórmula dos acréscimos finitos
de modo que (102) pode ser escrita
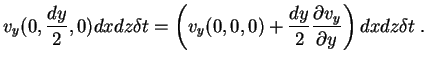 |
(103) |
A face oposta contribui com
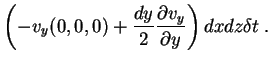 |
(104) |
de modo que a soma das duas é
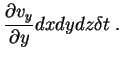 |
(105) |
Cada par de faces tem uma contribuição análoga. Somando
tudo, temos
Volume que sai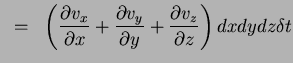 |
(106) |
Podemos então escrever que, por unidade de tempo,
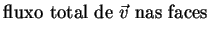 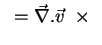 Volume do cubo Volume do cubo |
(107) |
Esta é a essência do teorema do divergente. Para um volume
delimitado por uma superfície fechada arbitrária,
tomando-se em cada ponto da superfície a normal externa,
temos
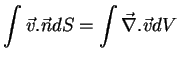 |
(108) |
Chega-se a este resultado ``reconstruíndo'' o volume (de
forma arbitrária), com cubinhos, como se fossem peças de um
Lego. Para cada cubinho vale o teorema, portanto vale para a soma.
Note-se que a superfície na qual se calcula o fluxo é a
superfície externa, pois cada superfície interna de um
cubinho pertence a dois cubinhos, e a contribuição de uma ao
fluxo cancela a da outra, já as normais têm sentido oposto.
Note-se que, tendo-se usado, da água, só a propriedade de que
suas velocidades formam um campo vetorial diferenciável, o teorema
é, na realidade, válido para quaisquer campos vetoriais
diferenciáveis. Vamos fazer uso amplo dele para os campos elétrico
e magnético, por exemplo.
Subsections



Next: O teorema de Helmholtz
Up: Campos vetoriais for the
Previous: O rotacional
Henrique Fleming
2003-08-11

![]() .
.