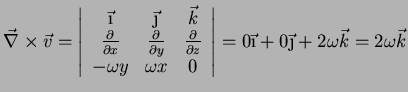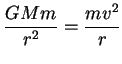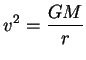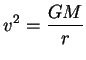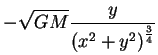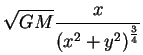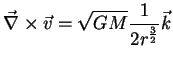Next: O teorema do divergente
Up: O operador diferencial
Previous: Exercícios
A partir do operador diferencial
 obtivemos o gradiente de um
campo escalar,
obtivemos o gradiente de um
campo escalar,
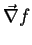 , e o divergente de um campo vetorial,
, e o divergente de um campo vetorial,
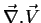 . Uma terceira operação possível é
a seguinte: seja
. Uma terceira operação possível é
a seguinte: seja
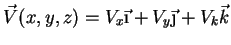 um campo
vetorial. O operador diferencial nabla é
Logo, pode-se pensar em definir
um campo
vetorial. O operador diferencial nabla é
Logo, pode-se pensar em definir
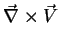 , o
produto vetorial de
, o
produto vetorial de
 pelo campo vetorial
pelo campo vetorial 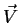 .
Temos
.
Temos
que dá, realizando os produtos vetoriais e simplificando,
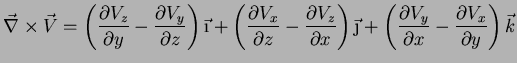 |
(87) |
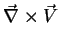 denomina-se o rotacional do campo vetorial
denomina-se o rotacional do campo vetorial
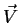 , e é, também ele, um campo vetorial.
, e é, também ele, um campo vetorial.
Como regra mnemônica costuma-se usar
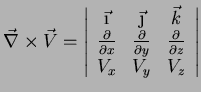 |
(88) |
Este determinante simbólico5 deve ser expandido, à maneira de Laplace, em
relação à primeira linha. Desta forma reproduz-se (87).
O leitor tem todo o direito de estar curioso. Que bichos são esses? Quando
é que um campo tem divergente zero? Quando é que tem rotacional zero?
Quando é que não tem? Por que todas essas definições?
Mais tarde, quando tivermos à disposição os teoremas integrais de
Gauss-Ostrogradskii e Stokes, poderemos mostrar com simplicidade o campo
vetorial típico com divergente zero e aquele com rotacional zero. Os
nomes desses operadores encontrarão também uma justificativa. Neste meio
tempo vamos apresentando alguns resultados parciais.
Exemplos:
(1) Um campo vetorial uniforme tem tanto o divergente quanto o
rotacional iguais a zero, pois as derivadas parciais de todas as
componentes são nulas.
(2) Considere o campo vetorial definido assim: seja 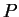 o ponto de
coordenadas (
o ponto de
coordenadas (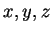 ). Toma-se o vetor que parte da origem até o ponto
). Toma-se o vetor que parte da origem até o ponto 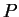 ,
e se o transporta, sempre paralelo a si mesmo, até que sua origem seja o
ponto
,
e se o transporta, sempre paralelo a si mesmo, até que sua origem seja o
ponto 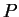 . Chamaremos este campo vetorial simplesmente de
. Chamaremos este campo vetorial simplesmente de 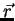 . Note
que o vetor associado à origem é o vetor
. Note
que o vetor associado à origem é o vetor 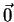 . Este campo tem
divergente não-nulo. De fato,
. Este campo tem
divergente não-nulo. De fato,
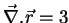 . Os vetores
``divergem'' a partir da origem. O rotacional deste campo é zero, como é
imediato verificar.
. Os vetores
``divergem'' a partir da origem. O rotacional deste campo é zero, como é
imediato verificar.
(3) Considere um disco rígido no plano 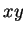 girando, com velocidade
angular constante, em torno do eixo
girando, com velocidade
angular constante, em torno do eixo 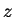 que passa pelo seu centro. Em cada
ponto do disco, seja
que passa pelo seu centro. Em cada
ponto do disco, seja 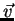 o vetor velocidade do ponto. Obtém-se
assim um campo de vetores que são tangentes a círculos de centro na
origem e que estão todos no plano
o vetor velocidade do ponto. Obtém-se
assim um campo de vetores que são tangentes a círculos de centro na
origem e que estão todos no plano 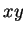 . Conseqüentemente,
. Conseqüentemente, 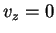 em
todos os pontos. Seja
em
todos os pontos. Seja
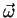 um vetor ao longo do eixo
um vetor ao longo do eixo 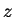 cujo
módulo é igual à velocidade angular
cujo
módulo é igual à velocidade angular 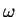 do disco, e cujo sentido
é o sentido positivo do eixo, se a rotação for
anti-horária. Então o campo vetorial pode ser descrito de uma forma
simples:
do disco, e cujo sentido
é o sentido positivo do eixo, se a rotação for
anti-horária. Então o campo vetorial pode ser descrito de uma forma
simples:
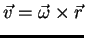 |
(89) |
Como
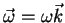 e
e
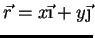 ,
,
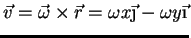 |
(90) |
O cálculo do rotacional dá:
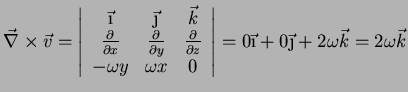 |
(91) |
O leitor não terá dificuldades em mostrar que, por outro lado,
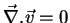 . O campo de vetores ``roda'', e o seu ``rotacional''
é diferente de zero. O rotacional foi introduzido pelo grande físico e
médico Hermann von Helmholtz para descrever turbilhões em fluidos, como os
tornados na atmosfera. Para uma descrição mais completa de seus grandes
trabalhos, veja ([15]).
. O campo de vetores ``roda'', e o seu ``rotacional''
é diferente de zero. O rotacional foi introduzido pelo grande físico e
médico Hermann von Helmholtz para descrever turbilhões em fluidos, como os
tornados na atmosfera. Para uma descrição mais completa de seus grandes
trabalhos, veja ([15]).
(4) Considere agora um disco de poeira cósmica girando em torno de uma
estrela, supondo, por simplicidade, órbitas circulares. Cada grão de
poeira é um planeta, e se move segundo as leis de Kepler. A que nos
interessa é a terceira, que é obtida impondo que a força de
atração gravitacional coincida com a força centrípeta.
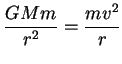 |
(92) |
ou
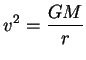 |
(93) |
(aqui, naturalmente, 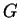 é a constante de gravitação universal, e
é a constante de gravitação universal, e 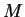 é a massa da estrela). No exemplo anterior vimos que um vetor tangente a um
círculo no plano
é a massa da estrela). No exemplo anterior vimos que um vetor tangente a um
círculo no plano 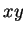 tem a forma
tem a forma
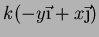 . Portanto,
podemos afirmar que a velocidade do grão de pó que está numa órbita
circular de raio
. Portanto,
podemos afirmar que a velocidade do grão de pó que está numa órbita
circular de raio 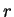 é
é
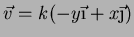 |
(94) |
com 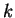 tal que
tal que
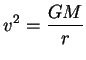 |
(95) |
Isto determina completamente o campo de velocidades, que é dado por
O cálculo do rotacional dá (bom exercício!)
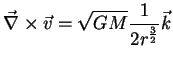 |
(98) |
É também um bom exercício mostrar que o divergente deste campo de
velocidades também é zero.
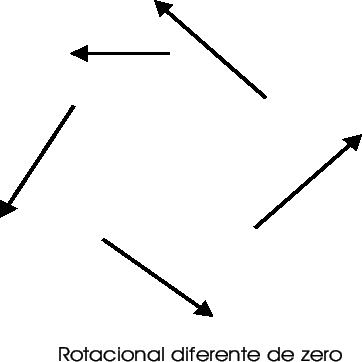
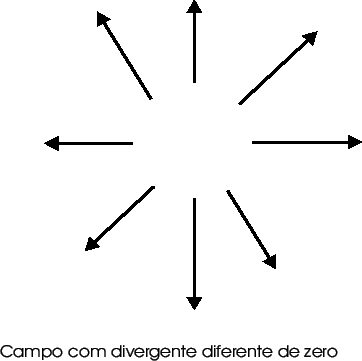
As figuras abaixo exibem campos típicos com rotacional
não-nulo e com divergente não-nulo.



Next: O teorema do divergente
Up: O operador diferencial
Previous: Exercícios
Henrique Fleming
2003-08-11
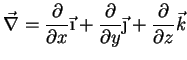
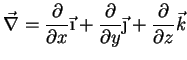
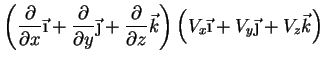
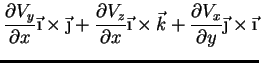
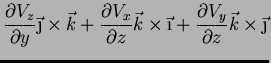
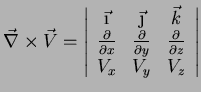
![]() o ponto de
coordenadas (
o ponto de
coordenadas (![]() ). Toma-se o vetor que parte da origem até o ponto
). Toma-se o vetor que parte da origem até o ponto ![]() ,
e se o transporta, sempre paralelo a si mesmo, até que sua origem seja o
ponto
,
e se o transporta, sempre paralelo a si mesmo, até que sua origem seja o
ponto ![]() . Chamaremos este campo vetorial simplesmente de
. Chamaremos este campo vetorial simplesmente de ![]() . Note
que o vetor associado à origem é o vetor
. Note
que o vetor associado à origem é o vetor ![]() . Este campo tem
divergente não-nulo. De fato,
. Este campo tem
divergente não-nulo. De fato,
![]() . Os vetores
``divergem'' a partir da origem. O rotacional deste campo é zero, como é
imediato verificar.
. Os vetores
``divergem'' a partir da origem. O rotacional deste campo é zero, como é
imediato verificar.
![]() girando, com velocidade
angular constante, em torno do eixo
girando, com velocidade
angular constante, em torno do eixo ![]() que passa pelo seu centro. Em cada
ponto do disco, seja
que passa pelo seu centro. Em cada
ponto do disco, seja ![]() o vetor velocidade do ponto. Obtém-se
assim um campo de vetores que são tangentes a círculos de centro na
origem e que estão todos no plano
o vetor velocidade do ponto. Obtém-se
assim um campo de vetores que são tangentes a círculos de centro na
origem e que estão todos no plano ![]() . Conseqüentemente,
. Conseqüentemente, ![]() em
todos os pontos. Seja
em
todos os pontos. Seja
![]() um vetor ao longo do eixo
um vetor ao longo do eixo ![]() cujo
módulo é igual à velocidade angular
cujo
módulo é igual à velocidade angular ![]() do disco, e cujo sentido
é o sentido positivo do eixo, se a rotação for
anti-horária. Então o campo vetorial pode ser descrito de uma forma
simples:
do disco, e cujo sentido
é o sentido positivo do eixo, se a rotação for
anti-horária. Então o campo vetorial pode ser descrito de uma forma
simples: