


Next: Derivadas direcionais
Up: Campos vetoriais: formulação moderna
Previous: Espaço Euclideano: conceitos básicos
2.1 Def. Um vetor tangente 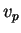 de
de
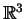 consiste de dois pontos
de
consiste de dois pontos
de
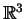 : a parte vetorial
: a parte vetorial 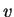 e o ponto de aplicação
e o ponto de aplicação 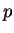 .
. 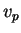 é sempre
representado pela flexa do ponto
é sempre
representado pela flexa do ponto 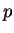 ao ponto
ao ponto 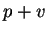 . É importante ressaltar que
dois vetores tangentes,
. É importante ressaltar que
dois vetores tangentes, 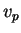 e
e 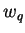 , são iguais,
, são iguais, 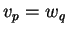 , se e só se
, se e só se
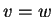 e
e 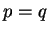 ; ou seja, além da igualdade das partes vetoriais, requer-se a
igualdade dos pontos de aplicação. Vetores com a mesma parte vetorial e pontos de
aplicação diferentes são ditos paralelos. Esta conceituação de vetores tangentes é
comum na física, onde o ponto de aplicação de uma força é essencial.
; ou seja, além da igualdade das partes vetoriais, requer-se a
igualdade dos pontos de aplicação. Vetores com a mesma parte vetorial e pontos de
aplicação diferentes são ditos paralelos. Esta conceituação de vetores tangentes é
comum na física, onde o ponto de aplicação de uma força é essencial.
2.2 Def.Seja 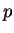 um ponto de
um ponto de
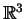 . O conjunto
. O conjunto
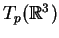 de todos os vetores que têm
de todos os vetores que têm 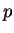 como ponto de aplicação é chamado de
espaço tangente a
como ponto de aplicação é chamado de
espaço tangente a
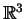 em
em 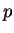 .
.
2.3 Def. Um campo vetorial 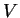 em
em
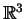 é uma função que associa a cada
ponto
é uma função que associa a cada
ponto 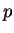 de
de
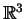 um vetor tangente
um vetor tangente 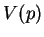 a
a
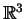 , em
, em 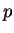 .
.
Existe uma álgebra natural para campos vetoriais:
onde
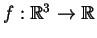
2.4 Def. Sejam
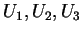 campos vetoriais em
campos vetoriais em
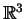 tais que
tais que
para todo
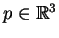 . Chamamos
. Chamamos
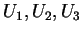 de referencial natural
de
de referencial natural
de
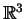 .
. 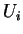 (
(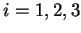 ) é um conjunto de vetores unitários
na direção
) é um conjunto de vetores unitários
na direção 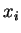 .
.
2.5 Lema Se 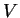 é um campo vetorial em
é um campo vetorial em
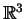 , existem três
( e só três) funções reais
, existem três
( e só três) funções reais
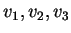 em
em
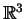 tais que
As funções
tais que
As funções
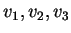 são denominadas funções coordenadas euclideanas de
são denominadas funções coordenadas euclideanas de 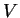 .
.
Prova
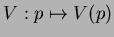 vetor tangente. A parte vetorial de
vetor tangente. A parte vetorial de 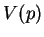 pode ser
descrita como
pode ser
descrita como
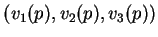 que, ponto a ponto, define as funções
que, ponto a ponto, define as funções
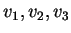 . Mas
. Mas
Logo,
Cálculos com campos vetoriais podem sempre ser expressos em termos de suas
funções coordenadas euclideanas. Por exemplo, a adição e a multiplicação por uma
função são dados por
Esta última equação significa que, em um ponto arbitrário 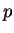 , teremos
Um campo vetorial
, teremos
Um campo vetorial 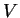 é diferenciável se suas funções coordenadas euclideanas
forem diferenciáveis.
é diferenciável se suas funções coordenadas euclideanas
forem diferenciáveis.



Next: Derivadas direcionais
Up: Campos vetoriais: formulação moderna
Previous: Espaço Euclideano: conceitos básicos
Henrique Fleming
2003-08-11
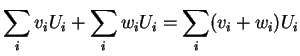
![$\displaystyle f\left[\sum_{i}v_iU_i\right]=\sum_{i}\left[fv_i\right]U_i$](img629.png)
![$\displaystyle \left\{f\left[\sum_{i}v_iU_i\right]\right\}(p)=\sum_{i}\left(
f(p)v_i(p)\right)U_i(p)
$](img630.png)