


Next: Curvas em
Up: Campos vetoriais: formulação moderna
Previous: Vetores Tangentes
Associada a cada vetor tangente
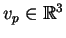 está a reta
Seja
está a reta
Seja 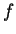 uma função diferenciável em
uma função diferenciável em
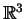 , e considere a função
que é uma função diferenciável na reta real. É claro que a derivada desta função de
, e considere a função
que é uma função diferenciável na reta real. É claro que a derivada desta função de 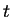 ,
em
,
em 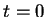 , nos diz como
, nos diz como 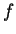 varia ao longo da reta que tem a direção de
varia ao longo da reta que tem a direção de 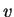 .
.
3.1 Def. Seja
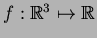 diferenciável, seja
diferenciável, seja 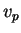 um vetor
tangente a
um vetor
tangente a
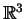 . O número
é a derivada de
. O número
é a derivada de 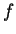 em relação a
em relação a 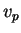 . Outra denominação usada é a de derivada
direcional na direção de
. Outra denominação usada é a de derivada
direcional na direção de 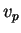 .
.
Exemplo:
e então
Para 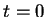 ,
O cálculo de
,
O cálculo de ![$ v_p[f]$](img650.png) pode ser reduzido ao cálculo das derivadas parciais no
ponto
pode ser reduzido ao cálculo das derivadas parciais no
ponto 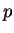 , como mostram os lemas a seguir.
, como mostram os lemas a seguir.
3.2 Lema Se
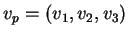 é um vetor tangente a
é um vetor tangente a
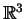 , então
Prova
, então
Prova
As principais propriedades dessa derivada direcional são:
3.3 Teorema Sejam
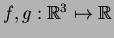 ,
, 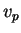 e
e 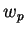 vetores tangentes,
vetores tangentes,
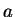 e
e 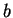 , números. Então,
, números. Então,
de demonstração imediata.
As primeiras duas propriedades podem ser sumarizadas assim: ![$ v_p[f]$](img650.png) é linear em
é linear em
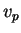 e em
e em 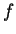 . A terceira é a propriedade de Leibnitz. Todos os tipos de
derivação que vamos encontrar têm essa característica: linearidade e Leibnitz.
. A terceira é a propriedade de Leibnitz. Todos os tipos de
derivação que vamos encontrar têm essa característica: linearidade e Leibnitz.
Dado um campo vetorial 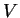 e uma função
e uma função 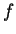 , podemos falar na função
, podemos falar na função ![$ V[f]$](img664.png) . De fato,
em cada ponto
. De fato,
em cada ponto 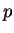 essa função tem o valor
essa função tem o valor ![$ V_p[f]$](img665.png) , ou seja, a derivada de
, ou seja, a derivada de 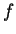 em
relação ao vetor tangente
em
relação ao vetor tangente 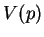 .
.
Seja
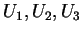 o campo de referenciais naturais em
o campo de referenciais naturais em
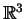 . Lembrando que
. Lembrando que
temos, evidentemente, que
![$ U_i[f]=\frac{\partial f}{\partial x^i}$](img669.png) .
.
Por exemplo:
3.4 Corolário. Sejam 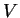 e
e 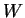 campos vetoriais em
campos vetoriais em
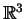 e
e 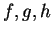 funções reais
funções reais
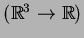 .
.
A demonstração é simples. Exemplo:
ou seja:
Para simplificar a notação, nem sempre vamos escrever o ponto de aplicação de um vetor
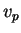 .
.



Next: Curvas em
Up: Campos vetoriais: formulação moderna
Previous: Vetores Tangentes
Henrique Fleming
2003-08-11
![$\displaystyle v_p[f]=\frac{d}{dt}\left(f(p+tv)\right)_{t=0}
$](img637.png)
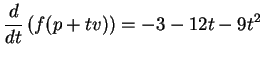
![$\displaystyle v_p[f]=\sum v_i\frac{\partial f}{\partial x_i}(p)
$](img652.png)
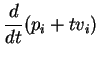
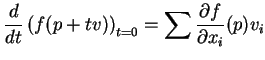
![]() e uma função
e uma função ![]() , podemos falar na função
, podemos falar na função ![]() . De fato,
em cada ponto
. De fato,
em cada ponto ![]() essa função tem o valor
essa função tem o valor ![]() , ou seja, a derivada de
, ou seja, a derivada de ![]() em
relação ao vetor tangente
em
relação ao vetor tangente ![]() .
.
![]() o campo de referenciais naturais em
o campo de referenciais naturais em
![]() . Lembrando que
. Lembrando que
![$\displaystyle U_1(p)[f]=\frac{d}{dt}\left(f(p_1+t,p_2,p_3)\right)_{t=0}=\frac{\partial f}{\partial
x^1}(p)
$](img670.png)