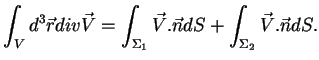Next: Fórmulas de Green
Up: A magia da equação
Previous: A magia da equação
Seja 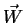 um campo vetorial ``bem comportado'',
um campo vetorial ``bem comportado'', 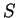 uma
superfície fechada, e
uma
superfície fechada, e 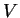 o volume interno a esta superfície.
Então,
o volume interno a esta superfície.
Então,
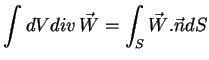 |
(172) |
onde 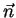 é a normal externa à superfície. Não vamos
demonstrar este teorema, mas usá-lo para demonstrar outros. Trata-se
de um teorema clássico da Análise. Uma demonstração moderna, usando
a teoria das formas diferenciais exteriores encontra-se em [1],
[2] ou [3]. Na aula apresentamos uma
``demonstração'' para o caso de um cubo, que serve para entender
a idéia central, num caso simples. Para a demonstração clássica,
o leitor não pode perder a oportunidade de consultar um dos grandes
livros de todos os tempos, o Treatise on Electricity and
Magnetism, de James Clerk Maxwell, ainda publicado pela Dover. Narrando
uma das maiores descobertas de todos os tempos, a natureza
eletromagnética da luz, esse livro, extraordinariamente bem escrito,
mantém ainda uma grande vivacidade e supera de muito todos
os epígonos modernos [4].
é a normal externa à superfície. Não vamos
demonstrar este teorema, mas usá-lo para demonstrar outros. Trata-se
de um teorema clássico da Análise. Uma demonstração moderna, usando
a teoria das formas diferenciais exteriores encontra-se em [1],
[2] ou [3]. Na aula apresentamos uma
``demonstração'' para o caso de um cubo, que serve para entender
a idéia central, num caso simples. Para a demonstração clássica,
o leitor não pode perder a oportunidade de consultar um dos grandes
livros de todos os tempos, o Treatise on Electricity and
Magnetism, de James Clerk Maxwell, ainda publicado pela Dover. Narrando
uma das maiores descobertas de todos os tempos, a natureza
eletromagnética da luz, esse livro, extraordinariamente bem escrito,
mantém ainda uma grande vivacidade e supera de muito todos
os epígonos modernos [4].
Na verdade, o teorema do divergente vale em situações mais gerais:
considere uma esfera da qual se subtrai o volume de uma esfera
concêntrica e menor. Seja 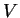 o volume externo à esfera pequena
e interno à grande; seja
o volume externo à esfera pequena
e interno à grande; seja 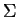 a superfície composta pela
superfície da esfera interna orientada pela normal interna,
denominada
a superfície composta pela
superfície da esfera interna orientada pela normal interna,
denominada 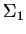 , e pela superfície da esfera grande, orientada
pela normal externa, denominada
, e pela superfície da esfera grande, orientada
pela normal externa, denominada 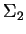 . Então, vale a seguinte
versão do teorema do divergente:
. Então, vale a seguinte
versão do teorema do divergente:
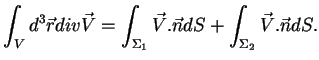 |
(173) |
É claro que as superfícies externa e interna não precisam
ser esféricas, e que o número de superfícies componentes
não se restringe a dois, podendo ser qualquer.



Next: Fórmulas de Green
Up: A magia da equação
Previous: A magia da equação
Henrique Fleming
2003-08-11
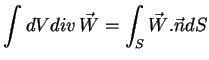
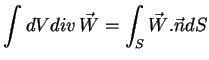
![]() o volume externo à esfera pequena
e interno à grande; seja
o volume externo à esfera pequena
e interno à grande; seja ![]() a superfície composta pela
superfície da esfera interna orientada pela normal interna,
denominada
a superfície composta pela
superfície da esfera interna orientada pela normal interna,
denominada ![]() , e pela superfície da esfera grande, orientada
pela normal externa, denominada
, e pela superfície da esfera grande, orientada
pela normal externa, denominada ![]() . Então, vale a seguinte
versão do teorema do divergente:
. Então, vale a seguinte
versão do teorema do divergente: