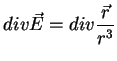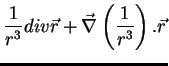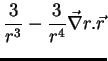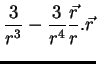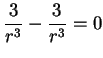Next: Cálculo vetorial for the
Up: O teorema do divergente
Previous: O teorema do divergente
À medida que formos nos aprofundando no eletromagnetismo não
poderemos deixar de notar a freqüência com que os operadoes
diferenciais div e rot aparecerão nas nossas equações.
O teorema de Helmholtz que descreveremos a seguir explica este fato. Por
enquanto não daremos uma demonstração dele. Na última parte destas
notas um tratamento detalhado (mas talvez um pouco avançado demais para
o terceiro semestre) deste e de outro teorema famoso de Helmholtz, porá a casa
em ordem. Por enquanto queremos entender o teorema. Provar é outra
coisa.6
Seja
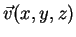 um campo vetorial que se anula no infinito. O teorema
de Helmholtz diz que este campo está completamente determinado se
conhecermos, em todos os pontos, as funções
um campo vetorial que se anula no infinito. O teorema
de Helmholtz diz que este campo está completamente determinado se
conhecermos, em todos os pontos, as funções
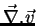 e
e
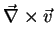 . Mais precisamente, sejam
. Mais precisamente, sejam 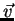 e
e 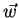 dois campos vetoriais que se anulam no infinito. Então, se
dois campos vetoriais que se anulam no infinito. Então, se
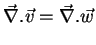 |
(109) |
e
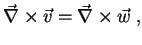 |
(110) |
segue que
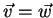 .
.
Exemplos:
(1)O exemplo mais trivial. Consideremos um campo vetorial 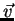 que se anula no
infinito e seja tal que
que se anula no
infinito e seja tal que
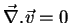 e
e
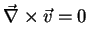 . Ora, o campo
. Ora, o campo 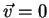 em todos os pontos
se anula no infinito (!) e tem rotacional e divergente nulos. Portanto, pelo
teorema de é o único que satisfaz a essas condições. Note-se que
a condição de se anular no infinito é essencial. De fato, um campo
uniforme, isto é,
em todos os pontos
se anula no infinito (!) e tem rotacional e divergente nulos. Portanto, pelo
teorema de é o único que satisfaz a essas condições. Note-se que
a condição de se anular no infinito é essencial. De fato, um campo
uniforme, isto é,
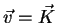 , onde
, onde 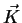 é um vetor constante,
tem também divergente e rotacional nulos. Logo, abrindo mão da condição
de se anular no infinito, existem infinitos campos com divergente e
rotacional nulos.
é um vetor constante,
tem também divergente e rotacional nulos. Logo, abrindo mão da condição
de se anular no infinito, existem infinitos campos com divergente e
rotacional nulos.
(2) Considere o campo vetorial
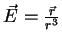 , que é
o campo elétrico de uma carga puntiforme de valor 1 colocada na origem.
Temos,
, que é
o campo elétrico de uma carga puntiforme de valor 1 colocada na origem.
Temos,
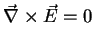 . Logo,
. Logo,
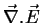 não pode ser zero. No entanto, se calcularmos, sem pensar muito, esse
divergente, acharemos o valor zero!. Vejam:
não pode ser zero. No entanto, se calcularmos, sem pensar muito, esse
divergente, acharemos o valor zero!. Vejam:
Onde está o erro? A função
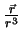 não é
contínua, e muito menos diferenciável, no ponto
não é
contínua, e muito menos diferenciável, no ponto 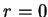 . Então
o resultado do nosso cálculo só vale para
. Então
o resultado do nosso cálculo só vale para 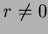 . E, de fato, veremos
depois que, usando métodos indiretos, podemos atribuir um valor (não nulo)
ao divergente deste campo na origem.
. E, de fato, veremos
depois que, usando métodos indiretos, podemos atribuir um valor (não nulo)
ao divergente deste campo na origem.
(3) Considere uma distribuição conínua de cargas, constante no
tempo, e que não se estende ao infinito. Neste caso, logo no
início do curso veremos que
o rotacional do campo elétrico é zero em todos os pontos, e que
o divergente desse campo é proporcional à densidade de carga elétrica.



Next: Cálculo vetorial for the
Up: O teorema do divergente
Previous: O teorema do divergente
Henrique Fleming
2003-08-11
![]() um campo vetorial que se anula no infinito. O teorema
de Helmholtz diz que este campo está completamente determinado se
conhecermos, em todos os pontos, as funções
um campo vetorial que se anula no infinito. O teorema
de Helmholtz diz que este campo está completamente determinado se
conhecermos, em todos os pontos, as funções
![]() e
e
![]() . Mais precisamente, sejam
. Mais precisamente, sejam ![]() e
e ![]() dois campos vetoriais que se anulam no infinito. Então, se
dois campos vetoriais que se anulam no infinito. Então, se