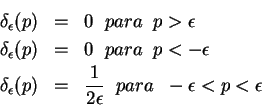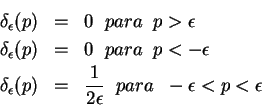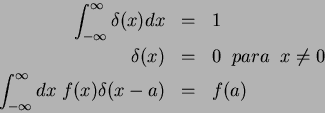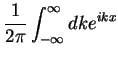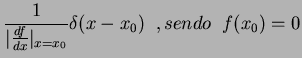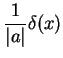Next: Integral de Fourier
Up: Algumas técnicas matemáticas
Previous: Algumas técnicas matemáticas
Considere a função
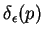 , definida assim:
, definida assim:
Temos, claramente,
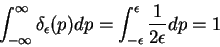 |
(33) |
Seja 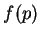 uma função contínua. Então,
uma função contínua. Então,
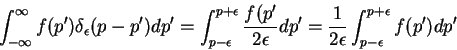 |
(34) |
No limite para
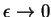 , esta última integral dá
, esta última integral dá
de forma que a Eq.(34) pode ser escrita
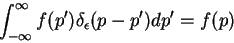 |
(35) |
A função delta de Dirac, 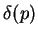 é definida, simbolicamente,
como o limite, para
é definida, simbolicamente,
como o limite, para
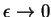 , da função
, da função
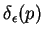 . Suas propriedades, que podem ser motivadas
por esse limite, podem ser sintetizadas assim:
. Suas propriedades, que podem ser motivadas
por esse limite, podem ser sintetizadas assim:
Nessas relações a integral não precisa realmente ir de 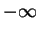 a
a
 . Basta que seja em um intervalo que contenha o ponto em
que o argumento da função delta se anula.
. Basta que seja em um intervalo que contenha o ponto em
que o argumento da função delta se anula.
Estritamente, tal função não existe. Trata-se de um símbolo que
abrevia muito os cálculos. Atendo-se às regras exibidas, nenhum
dano é causado, a não ser à lógica, a vítima usual. A teoria que
justifica essas operações e restitui a implacabilidade da lógica
foi desenvolvida pelo grande matemático francês Laurent Schwartz,
e se chama ``teoria das distribuições''. Para um tratamento
adequado da ``função delta'' recomendamos as notas que se
encontram no site do professor João Carlos Alves Barata,no
endereço:
http://denebola.if.usp.br/~jbarata/Notas_de_aula/arquivos/nc-cap12.pdf
Outras relações importantes envolvendo a ``função delta'' são as
seguintes:
onde, nesta última, se tem
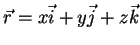 .
.



Next: Integral de Fourier
Up: Algumas técnicas matemáticas
Previous: Algumas técnicas matemáticas
Henrique Fleming
2003-03-30