


Next: Dois meios homogêneos
Up: Exemplos
Previous: Exemplos
de onde segue que
 , ou seja,
, ou seja,
Neste caso
e
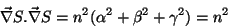 |
(17) |
Logo,
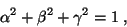 |
(18) |
e as superfícies
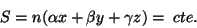 |
(19) |
são planos. Ora, as superfícies 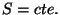 são as frentes de onda, logo
a propagação aqui descrita é a de ondas planas. Note-se que, se
são as frentes de onda, logo
a propagação aqui descrita é a de ondas planas. Note-se que, se 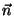 é um vetor unitário, isto é, se
é um vetor unitário, isto é, se
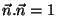 , temos, com
, temos, com
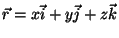 ,
,
e
Comparando com a Eq.(18) vemos que 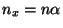 ,
, 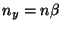 e
e
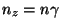 , razão pela qual
, razão pela qual 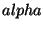 ,
, 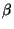 e
e 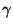 são os `` cosenos
diretores'' da direção
são os `` cosenos
diretores'' da direção 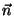 .
.
Henrique Fleming
2002-04-24