


Next: Obtenção do campo
A Relação de Clausius-Mossotti
Henrique Fleming
15 Agosto 2001
Quando um campo elétrico atua sobre um átomo, ou uma
molécula, causa um deslocamento das cargas positivas e
negativas que rompe o cancelamento exato das cargas. O efeito
dominante é a criação de um momento de dipolo elétrico.
Este fenômeno é denominado polarização. O efeito combinado
da polarização de todos os átomos é responsável pelas propriedades
elétricas dos dielétricos, ou isolantes.
Seja 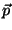 o momento de dipolo que a presença de um campo
elétrico externo
o momento de dipolo que a presença de um campo
elétrico externo 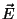 cria num átomo. Denomina-se
polarizabilidade do átomo a quantidade
cria num átomo. Denomina-se
polarizabilidade do átomo a quantidade 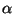 definida através
da equação
definida através
da equação
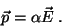 |
(1) |
Um modelo muito simples para o átomo dá, para a polarizabilidade,
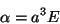 |
(2) |
onde 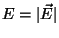 (Veja o Apêndice), sendo
(Veja o Apêndice), sendo 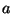 o raio do átomo.
Numa situação real, não temos um átomo isolado sob a ação de um
campo elétrico externo. Um átomo de um dielétrico está sob a ação
não só do campo externo, mas também sob a ação dos campos dos
outros átomos, que, agora polarizados, são capazes de agir uns sobre
os outros. Queremos saber que campo age sobre um átomo imerso
em um dielétrico polarizado. Como, naturalmente, o campo di próprio
átomo não age sobre ele mesmo, o que queremos saber é qual
é o valor do campo que existe na posição do átomo em questão.
Seja
o raio do átomo.
Numa situação real, não temos um átomo isolado sob a ação de um
campo elétrico externo. Um átomo de um dielétrico está sob a ação
não só do campo externo, mas também sob a ação dos campos dos
outros átomos, que, agora polarizados, são capazes de agir uns sobre
os outros. Queremos saber que campo age sobre um átomo imerso
em um dielétrico polarizado. Como, naturalmente, o campo di próprio
átomo não age sobre ele mesmo, o que queremos saber é qual
é o valor do campo que existe na posição do átomo em questão.
Seja 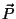 a polarização do dielétrico, que, como se sabe, é
o momento de dipolo elétrico por unidade de volume. Temos
a polarização do dielétrico, que, como se sabe, é
o momento de dipolo elétrico por unidade de volume. Temos
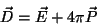 |
(3) |
e
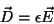 |
(4) |
para dielétricos simples. Logo,
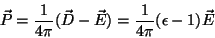 |
(5) |
O campo que age sobre um átomo é a soma do campo externo
aplicado sobre o dielétrico e dos campos que os demais átomos,
agora polarizados, produzem na posição do átomo considerado.
É dado por
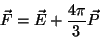 |
(6) |
como mostraremos mais abaixo. (Por enquanto, acredite neste resultado).
Como 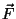 é o campo que age sobre um átomo, temos
é o campo que age sobre um átomo, temos
 |
(7) |
Seja 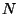 o número de átomos por unidade de volume. Então,
o número de átomos por unidade de volume. Então,
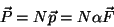 |
(8) |
Logo,
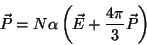 |
(9) |
e
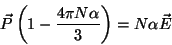 |
(10) |
Finalmente, usando
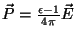 ,
,
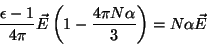 |
(11) |
de onde segue que
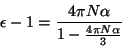 |
(12) |
ou, após um pouquinho de álgebra,
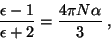 |
(13) |
que é a famosa relação de Clausius-Mossotti. A importância dessa
relação é que, do lado direito, temos quantidades relativas a um
átomo, enquanto que, do lado esquerdo, temos quantidades
macroscópicas. Clausius e Mossotti a descobriram no século XIX,
quando se falava ainda na hipótese atômica, e Ernst Mach defendia a
idéia de que se devia depurar a física de qualquer menção ao
hipotético átomo. A relação de Clausius-Mossotti permitiu, por
exemplo, ter-se uma idéia do tamanho do 'tomo. Voltaremos ao
assunto mais abaixo.



Next: Obtenção do campo
Henrique Fleming
2002-04-20