


Next: Histórico e aplicações
Up: A Relação de Clausius-Mossotti
Previous: A Relação de Clausius-Mossotti
Se o campo externo que age sobre o dielétrico é 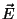 , o campo
sobre um átomo desse dielétrico será
, o campo
sobre um átomo desse dielétrico será
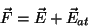 |
(14) |
onde 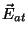 é o campo dos outros átomos na posição do átomo
em consideração. Em torno do átomo, imaginemos uma cavidade esférica
no dielétrico. O centro dessa cavidade é a posição do átomo. Dentro dela,
o vazio. O efeito dos campos de todos os outros átomos é criar, sobre a
superfície que delimita essa cavidade, uma certa distribuição superficial de
cargas. O campo que agirá sobre o átomo, devido aos outros átomos, é
o campo, criado por essas cargas, no centro da cavidade.
é o campo dos outros átomos na posição do átomo
em consideração. Em torno do átomo, imaginemos uma cavidade esférica
no dielétrico. O centro dessa cavidade é a posição do átomo. Dentro dela,
o vazio. O efeito dos campos de todos os outros átomos é criar, sobre a
superfície que delimita essa cavidade, uma certa distribuição superficial de
cargas. O campo que agirá sobre o átomo, devido aos outros átomos, é
o campo, criado por essas cargas, no centro da cavidade.
Cavidade esférica em um dielétrico.
A posição do átomo está marcada com um ponto.
Seja
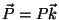 a polarização. Colocando a origem das coordenadas
no centro da esfera, temos que
a polarização. Colocando a origem das coordenadas
no centro da esfera, temos que
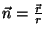 e
e
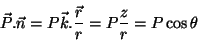 |
(15) |
Como vimos, a densidade superficial de cargas de polarização é,
precisamente,
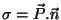 . Logo,
. Logo,
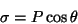 |
(16) |
O campo desta distribuição de cargas no centro da esfera é dado
por
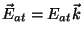 , com
, com
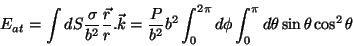 |
(17) |
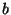 sendo o raio da esfera. Logo,
sendo o raio da esfera. Logo,
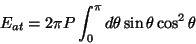 |
(18) |
isto é,
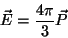 |
(19) |
como tínhamos antecipado.



Next: Histórico e aplicações
Up: A Relação de Clausius-Mossotti
Previous: A Relação de Clausius-Mossotti
Henrique Fleming
2002-04-20
(10,0...
...vec{E}$}
\uput[0](6.2,2.8){$\vec{k}$}
\psline{->}(6,3)(6.5,3)
\end{pspicture}](img26.png)