


Next: Bibliography
Up: A Relação de Clausius-Mossotti
Previous: Obtenção do campo
A relação de Clausius-Mossotti é escrita
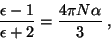 |
(20) |
Embora tenhamos sempre falado em átomos, a maior parte das substâncias
se organiza em moléculas, que são neutras e se polarizam, como os átomos.
Assim, a mesma fórmula vale também se 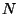 é o número de
moléculas por unidade de volume. Seja
é o número de
moléculas por unidade de volume. Seja 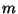 a massa de uma molécula.
Multiplicando numerador e denominador por
a massa de uma molécula.
Multiplicando numerador e denominador por 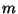 temos, do lado direito,
o produto
temos, do lado direito,
o produto 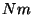 , que é a massa por unidade de volume, ou seja, a
densidade
, que é a massa por unidade de volume, ou seja, a
densidade 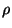 . Ao mesmo tempo aparece
. Ao mesmo tempo aparece
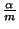 , uma nova
constante, característica da molécula. Para dielétricos gasosos
diluídos, temos sempre
, uma nova
constante, característica da molécula. Para dielétricos gasosos
diluídos, temos sempre
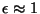 , de maneira que
, de maneira que
e, então, a relação de Clausius-Mossotti se lê:
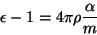 |
(21) |
que permite a determinação de
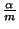 . Medindo-se a massa da
molécula pode-se, então determinar
. Medindo-se a massa da
molécula pode-se, então determinar 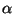 , que, como vimos,
é aproximadamente
, que, como vimos,
é aproximadamente 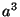 , sendo
, sendo 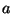 o raio da molécula. No começo
do século Einstein propôs diversas maneiras de medir a massa de
moléculas (estudando o movimento browniano, por exemplo). Com isso,
então, pode-se determinar o raio delas. Para gases, temos a seguinte maneira:
1 mol de gás possui o número de Avogadro de moléculas,
o raio da molécula. No começo
do século Einstein propôs diversas maneiras de medir a massa de
moléculas (estudando o movimento browniano, por exemplo). Com isso,
então, pode-se determinar o raio delas. Para gases, temos a seguinte maneira:
1 mol de gás possui o número de Avogadro de moléculas,
Logo, a massa de uma molécula é dada por
Aqui usamos a convecção, proposta por Sommerfeld, de denotar o
número de Avogadro por 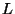 , em homenagem a Loschmidt, que foi a
primeira pessoa a medí-lo. Assim evitamos também o embaraço
de usar a letra
, em homenagem a Loschmidt, que foi a
primeira pessoa a medí-lo. Assim evitamos também o embaraço
de usar a letra 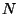 para duas coisas diferentes.
Clausius é bem conhecido, pelos seus trabalhos ligados à segunda lei
da termodinâmica. Mossotti se tornou conhecido por este trabalho. Sua
publicação, de 1850, tratava a molécula como uma esfera condutora!
O tópico que tratamos aqui encontra-se em quase todos os textos. É
um tema clássico. Não obstante, é raro achar-se um tratamento
adequado. O próprio Feynman é obscuro, neste ponto (sua dedução
é excessivamente artificial). O tratamento que seguimos é o de
Sommerfeld, do volume 3 de seu tratado de Física Teórica[1], que
é uma referência maravilhosa, cheia de notas históricas e
comentários interessantes, que dão vida à física1. E se a física
não tiver vida, terá o que, morte?
para duas coisas diferentes.
Clausius é bem conhecido, pelos seus trabalhos ligados à segunda lei
da termodinâmica. Mossotti se tornou conhecido por este trabalho. Sua
publicação, de 1850, tratava a molécula como uma esfera condutora!
O tópico que tratamos aqui encontra-se em quase todos os textos. É
um tema clássico. Não obstante, é raro achar-se um tratamento
adequado. O próprio Feynman é obscuro, neste ponto (sua dedução
é excessivamente artificial). O tratamento que seguimos é o de
Sommerfeld, do volume 3 de seu tratado de Física Teórica[1], que
é uma referência maravilhosa, cheia de notas históricas e
comentários interessantes, que dão vida à física1. E se a física
não tiver vida, terá o que, morte?



Next: Bibliography
Up: A Relação de Clausius-Mossotti
Previous: Obtenção do campo
Henrique Fleming
2002-04-20