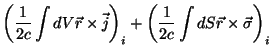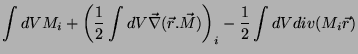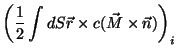Next: Apêndice
Up: Magnetismo da matéria
Previous: Correntes superficiais
Consideremos distribuições de correntes tais que
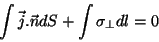 |
(27) |
Vamos mostrar que há soluções distintas de 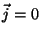 e
e
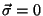 .
De fato, sejam
.
De fato, sejam
Vamos mostrar que, qualquer que seja a superfície 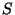 e qualquer que seja a
curva fechada
e qualquer que seja a
curva fechada 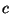 em torno da superfície,
em torno da superfície,
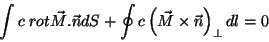 |
(30) |
A primeira integral dá, pelo teorema de Stokes,
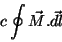 |
(31) |
e a segunda, pelo que vimos na seção anterior,
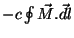 . Logo,
a Eq.(30) é satisfeita. Note-se que pode haver compensação: os dois termos não
precisam ser, separadamente, nulos.
Vamos agora calcular o momento magnético de dipolo devido a ambas as correntes. É praticamente
uma repetição de cálculo feito anteriormente. A i-ésima componente de
. Logo,
a Eq.(30) é satisfeita. Note-se que pode haver compensação: os dois termos não
precisam ser, separadamente, nulos.
Vamos agora calcular o momento magnético de dipolo devido a ambas as correntes. É praticamente
uma repetição de cálculo feito anteriormente. A i-ésima componente de 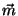 é:
é:
Como
temos
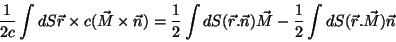 |
(34) |
Além disso,
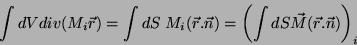 |
(35) |
Logo, temos precisamente
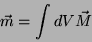 |
(36) |
e, assim, também quando se consideram as correntes superficiais, a magnetização é o momento de
dipolo magnético por unidade de volume.
Como a relação definidora de 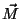 envolve só o seu rotacional, podemos construir
infinitos
envolve só o seu rotacional, podemos construir
infinitos 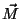 equivalentes adicionando a um deles o gradiente de uma função
arbitrária, pois
equivalentes adicionando a um deles o gradiente de uma função
arbitrária, pois
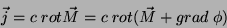 |
(37) |
e
Vamos mostrar que
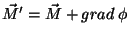 ainda é solução da
Eq.(27). De fato, vimos que o último termo dessa
equação pode ser escrito, quando se insere a expressão para
ainda é solução da
Eq.(27). De fato, vimos que o último termo dessa
equação pode ser escrito, quando se insere a expressão para
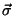 em termos de
em termos de 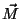 , como
, como
 |
(38) |
Acrescentando-se a 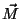 um termo da forma
um termo da forma 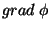 teremos,
na última equação, a adição de um termo
teremos,
na última equação, a adição de um termo
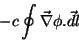 |
(39) |
que é zero, pois
e
Logo, a Eq.(27) ainda é satisfeita. A densidade de corrente 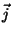 não é alterada pela adição do gradiente, mas a densidade superficial de corrente
é. Logo, a flexibilidade na escolha de
não é alterada pela adição do gradiente, mas a densidade superficial de corrente
é. Logo, a flexibilidade na escolha de 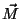 efetivamente não existe, pois
os diversos
efetivamente não existe, pois
os diversos 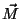 possíveis correspondem a densidades superficiais de correntes
diferentes, e elas são quantidades mensuráveis. Este fato não é só de
interesse acadêmico: note que
possíveis correspondem a densidades superficiais de correntes
diferentes, e elas são quantidades mensuráveis. Este fato não é só de
interesse acadêmico: note que
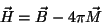 |
(40) |
de maneira que, se 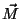 tiver alguma ambigüidade,
tiver alguma ambigüidade, 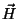 também terá.
também terá.



Next: Apêndice
Up: Magnetismo da matéria
Previous: Correntes superficiais
Henrique Fleming
2002-04-22