


Next: Interpretação de
Up: Magnetismo da matéria
Previous: A magnetização
Para uma classe muito importante de materiais existe uma relação muito
simples entre 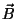 e
e 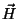 :
:
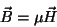 |
(13) |
onde 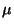 é uma quantidade característica da substância, denominada
permeabilidade magnética. Esta relação não é uma lei básica
do magnetismo, como, por exemplo,
é uma quantidade característica da substância, denominada
permeabilidade magnética. Esta relação não é uma lei básica
do magnetismo, como, por exemplo, 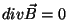 , mas sim uma propriedade
de uma classe específica de substâncias. Relações deste tipo, que
suplementam as equações de Maxwell, chama-se equações
constitutivas. Os materiais que satisfazem
a Eq.(13) chama-se diamagnéticos ou paramagnéticos. Os
diamagnéticos se assemelham aos dielétricos: fazem decrescer o valor
do campo. Os paramagnéticos têm o efeito contrário. Uma outra classe
importante de materiais magnéticos é constituída pelos ferromagnéticos,
materiais que amplificam enormemente o valor do campo magnético que age
sobre eles. A relação entre
, mas sim uma propriedade
de uma classe específica de substâncias. Relações deste tipo, que
suplementam as equações de Maxwell, chama-se equações
constitutivas. Os materiais que satisfazem
a Eq.(13) chama-se diamagnéticos ou paramagnéticos. Os
diamagnéticos se assemelham aos dielétricos: fazem decrescer o valor
do campo. Os paramagnéticos têm o efeito contrário. Uma outra classe
importante de materiais magnéticos é constituída pelos ferromagnéticos,
materiais que amplificam enormemente o valor do campo magnético que age
sobre eles. A relação entre 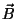 e
e 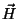 para ferromagnetos é muito
mais complicada, sendo altamente não-linear.
Como exemplo do uso das equações constitutivas, vamos calcular o valor do
campo magnético no interior de um solenóide dentro do qual foi
inserido um cilindro de material magnético de permeabilidade
para ferromagnetos é muito
mais complicada, sendo altamente não-linear.
Como exemplo do uso das equações constitutivas, vamos calcular o valor do
campo magnético no interior de um solenóide dentro do qual foi
inserido um cilindro de material magnético de permeabilidade 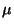 .
Neste caso a determinação de
.
Neste caso a determinação de 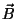 é muito complicada, pois
teríamos de levar em conta as correntes microscópicas que nascem
na substância sob a ação do campo do solenoide. Para
é muito complicada, pois
teríamos de levar em conta as correntes microscópicas que nascem
na substância sob a ação do campo do solenoide. Para 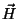 , por
outro lado, essas correntes microscópicas são irrelevantes. Se o
material inserido não quebrar a simetria do problema, podemos
calcular
, por
outro lado, essas correntes microscópicas são irrelevantes. Se o
material inserido não quebrar a simetria do problema, podemos
calcular 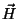 usando a lei circuital de Ampère, da mesma forma
que a usamos para calcular
usando a lei circuital de Ampère, da mesma forma
que a usamos para calcular 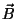 para o solenoide vazio. Obtemos
(detalhes no Apêndice)
para o solenoide vazio. Obtemos
(detalhes no Apêndice)
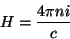 |
(14) |
e, então,
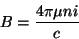 |
(15) |
onde usamos, na última passagem, a equação constitutiva.



Next: Interpretação de
Up: Magnetismo da matéria
Previous: A magnetização
Henrique Fleming
2002-04-22