


Next: Bibliography
Up: Apêndice
Previous: Cálculo do de um
Seja 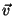 um campo vetorial uniforme (ou seja, constante espacialmente), e
um campo vetorial uniforme (ou seja, constante espacialmente), e 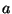 um campo escalar (uma função real). Vamos aplicar o teorema do divergente ao campo
vetorial
um campo escalar (uma função real). Vamos aplicar o teorema do divergente ao campo
vetorial 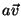 . Temos
. Temos
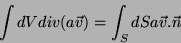 |
(49) |
Por outro lado,
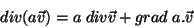 |
(50) |
e, como 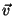 é constante,
é constante,
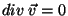 . Logo,
. Logo,
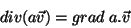 |
(51) |
Levando este resultado à Eq.(49), temos
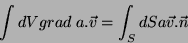 |
(52) |
Mas 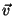 é constante, portanto pode ser colocado fora das integrais:
é constante, portanto pode ser colocado fora das integrais:
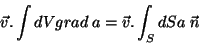 |
(53) |
Como 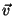 é arbitrário (fora o fato de ser constante), temos
é arbitrário (fora o fato de ser constante), temos
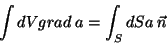 |
(54) |
Henrique Fleming
2002-04-22