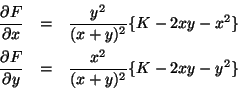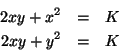Next: Multiplicadores de Lagrange
Up: O método
Previous: O método
Seja 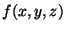 a função da qual queremos saber os máximos e
mínimos, e seja
a função da qual queremos saber os máximos e
mínimos, e seja
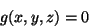 |
(1) |
a condição subsidiária. No problema citado acima, teríamos
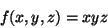 |
(2) |
e 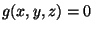 seria dada por
seria dada por
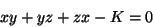 |
(3) |
Desta última relação segue que
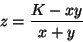 |
(4) |
que, levada à Eq.(2), dá:
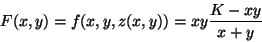 |
(5) |
A solução é obtida agora igualando a zero as derivadas parcias
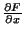 e
e
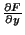 , que
são
, que
são
Igualadas a zero, obtemos as equações
de onde se conclui que 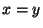 e que
e que 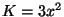 . Logo,
temos também
. Logo,
temos também 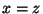 , ou seja, o paralelepípedo de volume
máximo, para área dada, é o cubo (existem soluções para o volume
mínimo. Quais são?).
, ou seja, o paralelepípedo de volume
máximo, para área dada, é o cubo (existem soluções para o volume
mínimo. Quais são?).



Next: Multiplicadores de Lagrange
Up: O método
Previous: O método
Henrique Fleming
2003-09-24