


Next: About this document ...
Up: Apêndice
Previous: Uma derivada importante
Vamos introduzir a notação
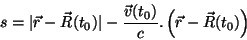 |
(64) |
Usando-a, tem-se, para os potenciais de Liénard-Wiechert (13) e
(14),
O campo elétrico é escrito em termos dos potenciais como:
Cálculo de
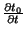 :
:
Mas
![\begin{displaymath}
\frac{\partial}{\partial t}\vert\vec{r}-\vec{R}(t_0)\vert=\...
...\vec{r}].\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(t_0)\vert} \; ,
\end{displaymath}](img129.png) |
(73) |
logo,
![\begin{displaymath}
\frac{[\vec{R}(t_0)-\vec{r}].\vec{v}(t_0)}
{\vert\vec{r}-\...
...partial t_0}{\partial t}-c+c\frac{\partial t_0}{\partial t}=0
\end{displaymath}](img130.png) |
(74) |
de onde segue imediatamente que
![\begin{displaymath}
\frac{\partial t_0}{\partial t}=\frac{1}{1-\frac{[\vec{r}-\vec{R}(t_0)].\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(t_0)\vert c}}
\end{displaymath}](img131.png) |
(75) |
Conseqüentemente,
Como
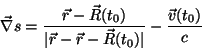 |
(79) |
temos, juntando tudo,
Aqui vemos o campo elétrico dividido claramente em duas partes: a primeira cai com
a quadrado da distância; a segunda, que cai linearmente com a distância, é o
campo de radiação. Existe apenas quando 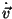 é diferente de zero, ou
seja, quando a carga é acelerada.
é diferente de zero, ou
seja, quando a carga é acelerada.



Next: About this document ...
Up: Apêndice
Previous: Uma derivada importante
Henrique Fleming
2002-04-20
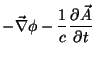
![$\displaystyle -e\left[\vec{\nabla}\frac{1}{s}+\frac{1}{c}\frac{\partial}{\partial t}\frac{\vec{v}}{cs}
\right]$](img122.png)
![$\displaystyle -e\left[-\frac{1}{s^2}\vec{\nabla}s+\frac{1}{c^2}\dot{\vec{v}}(t_...
..._0)}{s^2}\frac{\partial s}{\partial t_0}
\frac{\partial t_0}{\partial t}\right]$](img123.png)
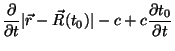
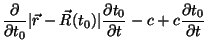
![\begin{displaymath}
\frac{\partial}{\partial t}\vert\vec{r}-\vec{R}(t_0)\vert=\...
...\vec{r}].\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(t_0)\vert} \; ,
\end{displaymath}](img129.png)
![\begin{displaymath}
\frac{[\vec{R}(t_0)-\vec{r}].\vec{v}(t_0)}
{\vert\vec{r}-\...
...partial t_0}{\partial t}-c+c\frac{\partial t_0}{\partial t}=0
\end{displaymath}](img130.png)
![\begin{displaymath}
\frac{\partial t_0}{\partial t}=\frac{1}{1-\frac{[\vec{r}-\vec{R}(t_0)].\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(t_0)\vert c}}
\end{displaymath}](img131.png)
![$\displaystyle \frac{\partial}{\partial t_0}\left[
\vert\vec{r}-\vec{R}(t_0)\vert-\frac{\vec{v}(t_0)}{c}.(\vec{r}-\vec{R}(t_0))\right]$](img133.png)
![$\displaystyle \frac{[\vec{r}-\vec{R}(t_0)].\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(...
...t{\vec{v}}(t_0)}{c}.\left(\vec{r}-\vec{R}(t_0)\right)
+\frac{\vec{v}^2(t_0)}{c}$](img134.png)
![$\displaystyle -e\left(-\frac{1}{s^2}\vec{\nabla}s+\frac{1}{c^2}
\dot{\vec{v}}(t...
...[\vec{r}-\vec{R}(t_0)].\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(t_0)\vert c}}\right)$](img135.png)
![$\displaystyle e\left(\frac{1}{c^2}\frac{\vec{v}}{s^2}\left[\frac{[\vec{r}-\vec{...
...\vec{r}-\vec{R}(t_0)].
\vec{v}(t_0)}
{\vert\vec{r}-\vec{R}(t_0)\vert c}}\right)$](img137.png)
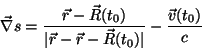
![$\displaystyle e\left[-\frac{1-\left(\frac{v}{c}\right)^2}{s^3}
\{(\vec{R}-\vec{r})+\frac{\vec{v}}{c}\vert\vec{R}-\vec{r}\vert\}\right]_{t_0}$](img139.png)
![$\displaystyle e\left[\frac{1}{s^3c^2}(\vec{R}-\vec{r})\times\left(
(\vec{R}-\ve...
...c{\vec{v}}{c}\vert\vec{R}-\vec{r}\vert)\times \dot{\vec{v}}\right)\right]_{t_0}$](img141.png)