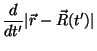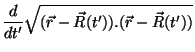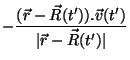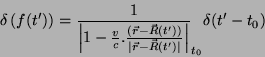Next: Os campos de Liénard-Wiechert
Up: Apêndice
Previous: Apêndice
Nesta seção realizamos em detalhe o cálculo prometido acima.
A função cuja derivada (em 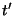 ) devemos calcular é:
) devemos calcular é:
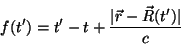 |
(58) |
Temos
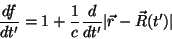 |
(59) |
Mas
Logo,
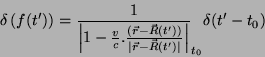 |
(63) |
como prometido.
Henrique Fleming
2002-04-20