


Next: Apêndice
Up: O dipolo de Hertz
Previous: O vetor de Poynting
Usando a notação exponencial a quantidade complexa cuja parte real
é
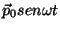 é
é
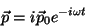 |
(52) |
O campo elétrico produzido pelo dipolo oscilante pode então ser
escrito
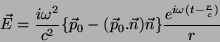 |
(53) |
e, lembrando que
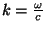 , podemos escrever
, podemos escrever
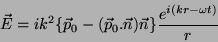 |
(54) |
Suponhamos que a direção de observação seja perpendicular a 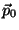 .
Então,
.
Então,
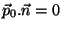 e
e
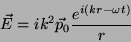 |
(55) |
e, para 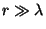 ,
,
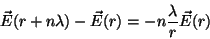 |
(56) |
o que mostra que o módulo de 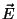 só varia sensivelmente
se
só varia sensivelmente
se 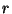 tem seu valor aumentado de um grande número de comprimentos
de onda. Ou seja, a grandes distâncias a onda produzida por um dipolo
oscilante é aproximadamente plana. O termo
tem seu valor aumentado de um grande número de comprimentos
de onda. Ou seja, a grandes distâncias a onda produzida por um dipolo
oscilante é aproximadamente plana. O termo
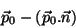 |
(57) |
que aparece na expressão de 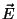 tem uma interpretação geométrica
simples, mostrada na figura abaixo.
De uma maneira geral, cada observador (olhando de
tem uma interpretação geométrica
simples, mostrada na figura abaixo.
De uma maneira geral, cada observador (olhando de 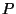 na direção
na direção
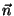 ) ``vê'' um dipolo de módulo igual à projeção do
verdadeiro dipolo na direção perpendicular a
) ``vê'' um dipolo de módulo igual à projeção do
verdadeiro dipolo na direção perpendicular a 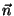 . O campo
elétrico que o atinge é proporcional a essa projeção; a intensidade
é proporcional ao quadrado dela. Assim, tanto em intensidade quanto
em polarização, é a projeção do momento de dipolo na direção perpendicular
à de observação que determina tudo. Em particular, olhando-se
na direção do próprio dipolo, não se deteta nenhum campo de
radiação.
. O campo
elétrico que o atinge é proporcional a essa projeção; a intensidade
é proporcional ao quadrado dela. Assim, tanto em intensidade quanto
em polarização, é a projeção do momento de dipolo na direção perpendicular
à de observação que determina tudo. Em particular, olhando-se
na direção do próprio dipolo, não se deteta nenhum campo de
radiação.



Next: Apêndice
Up: O dipolo de Hertz
Previous: O vetor de Poynting
Henrique Fleming
2002-04-20
![\begin{pspicture}(0,0)(10,6)
\psline[linewidth=2pt]{->}(0,0)(0,1)
\psline{->}(...
...eta$}
\uput[0](1,0.5){$\vec{n}$}
\uput[0](5.5,3.2){$\vec{r}$}
\end{pspicture}](img102.png)
![\begin{pspicture}(0,0)(10,6)
\psline[linewidth=2pt]{->}(3,0)(3,2)
\psline[line...
..._0$}
\uput[0](4.8,1.5){$\vec{n}$}
\uput[0](8,5){${\Large P}$}
\end{pspicture}](img108.png)