


Next: Aspecto dos campos produzidos
Up: O dipolo de Hertz
Previous: O dipolo de Hertz
Temos
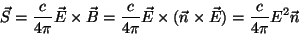 |
(46) |
Se o ângulo entre 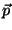 e
e 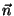 for
for 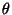 , teremos então
, teremos então
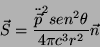 |
(47) |
ou ainda, explicitando a dependência no tempo,
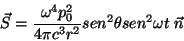 |
(48) |
A potência média por 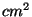 por período é dada por
por período é dada por
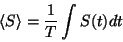 |
(49) |
onde 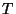 é o período. Lembrando que
é o período. Lembrando que
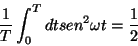 |
(50) |
temos
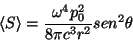 |
(51) |
Uma conclusão importante é que o dipolo oscilante tem uma
potência que depende fortemente da freqüência (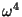 !). Isto
é a base da explicação de Rayleigh para a cor azul do céu2.
!). Isto
é a base da explicação de Rayleigh para a cor azul do céu2.
Lord Rayleigh foi um dos maiores físicos da virada do século XIX
para o XX. É tido como o maior dos físico-matemáticos, mas mesmo
isto o diminuiria, pois fez também descobertas experimentais muito
importantes, como a do elemento argônio. Sua obra mais famosa
é um grande tratado sobre a Acústica, The Theory of Sound. Sendo
um homem muito rico, trabalhava, e tinha seus laboratórios, em
um sítio nos arredores de Londres. Sua irmã era casada com Lord
Balfour, um dos mais famosos primeiros-ministros da Inglaterra. Entre
os muitos documentos manuscritos que deixou, encontram-se alguns
escritos no verso de folhas com o timbre Downing Street 10, que é
o enderço do primeiro-ministro. Tony Blair mora lá. Usava-os como
rascunho!



Next: Aspecto dos campos produzidos
Up: O dipolo de Hertz
Previous: O dipolo de Hertz
Henrique Fleming
2002-04-20