


Next: A Relatividade de Einstein
Up: A Relatividade de Galileu
Previous: A Relatividade de Galileu
Uma transformação que altera a fase de todos os estados por um mesmo valor, é
equivalente à identidade, na mecânica quântica. Então, quando a ordem em que
duas transformações são aplicadas é irrelevante, não segue necessariamente que o
comutador é zero: ele pode ser da forma
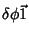 (que inclui zero como
um caso particular).
(que inclui zero como
um caso particular).
A determinação de
![$\delta_{[12]}\phi$](img306.png) não pode se basear em considerações
geométricas, que são clássicas. Temos que determiná-la exigindo a consistência
do formalismo.
não pode se basear em considerações
geométricas, que são clássicas. Temos que determiná-la exigindo a consistência
do formalismo.
A expressão mais geral para
![$\delta_{[12]}\phi=-\delta_{[21]}\phi$](img307.png) é
é
onde 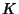 ,
, 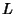 e
e 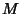 são constantes. Considere a identidade de Jacobi
são constantes. Considere a identidade de Jacobi
![\begin{displaymath}[[G_1,G_2],g_3]+[[G_3,G_1],G_2]+[[G_2,G_3],G_1]=0
\end{displaymath}](img316.png) |
(153) |
que pode ser escrita
![\begin{displaymath}
G_{[[123]}+G_{[[31]2]}+G_{[[23]1]}=0
\end{displaymath}](img317.png) |
(154) |
e, como
![\begin{displaymath}
G_{[12]}=\delta_{[12]}\lambda_a G_a
\end{displaymath}](img318.png) |
(155) |
temos
![\begin{displaymath}
\delta_{[[12]3]}\lambda_a+\delta_{[[31]2]}\lambda_a+\delta_{[[23]1]}\lambda_a=0
\end{displaymath}](img319.png) |
(156) |
para cada 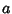 , e, em particular, para
, e, em particular, para
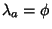 . Usando então a expresão
para
. Usando então a expresão
para
![$\delta_{[12]}\phi$](img306.png) , temos
, temos
Um cálculo explícito mostra que o coeficiente de 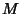 é zero, enquanto que
os de
é zero, enquanto que
os de 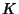 e
e 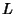 não são identicamente nulos. Logo, a identidade de Jacobi força
não são identicamente nulos. Logo, a identidade de Jacobi força
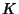 e
e 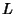 a serem nulos, permitindo, porém, que
a serem nulos, permitindo, porém, que 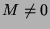 . Logo,
. Logo,
![\begin{displaymath}
\delta_{[12]}\phi=M\left(\delta_1\vec{\epsilon}.\delta_2\vec{v}-\delta_2\vec{\epsilon}.
\delta_1\vec{v}\right)
\end{displaymath}](img326.png) |
(158) |



Next: A Relatividade de Einstein
Up: A Relatividade de Galileu
Previous: A Relatividade de Galileu
Henrique Fleming
2001-12-26
![]() não pode se basear em considerações
geométricas, que são clássicas. Temos que determiná-la exigindo a consistência
do formalismo.
não pode se basear em considerações
geométricas, que são clássicas. Temos que determiná-la exigindo a consistência
do formalismo.
![]() é
é