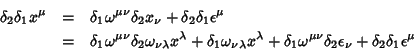Next: About this document ...
Up: Simetrias fundamentais
Previous: A questão do termo
As transformações de Lorentz são transformações lineares
homogêneas que mantêm invariante aforma quadrática
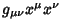 . Escrevendo
. Escrevendo
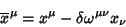 |
(159) |
a condição de invariância impõe que
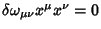 , ou seja,
, ou seja,
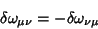 |
(160) |
Conclusão: as transformações infinitesimais de Lorentz são
transformações do tipo
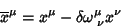 |
(161) |
com
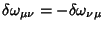 .
.
As transformações de Poincaré são as transformações de
Lorenyz e mais quatro translações, ou seja:
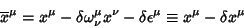 |
(162) |
e formam um grupo de 10 parâmetros. A relação com os parâmetros do grupo de Galileu vem através de
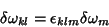 |
(163) |
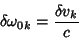 |
(164) |
A composição de parâmetros é obtida lembrando que
![\begin{displaymath}
\delta_{[12]}x^\mu=\delta_2\delta_1x^\mu-\delta_1\delta_2x^\mu
\end{displaymath}](img336.png) |
(165) |
Mas
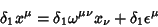 |
(166) |
Então
de modo que
Os comutadores da álgebra de Lie podem ser calculados agora da forma
usual, pondo-se
![\begin{displaymath}
\delta_{[12]}\lambda_a G_a=\frac{1}{i}[\delta_1\lambda_b
G_b,\delta_2\lambda_c G_c]
\end{displaymath}](img345.png) |
(170) |
e
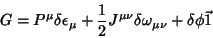 |
(171) |
Contudo,
![$\delta_{[12]}\phi$](img306.png) neste caso é zero, porque é
impossível construir uma forma bilinear antissimétrica
(
neste caso é zero, porque é
impossível construir uma forma bilinear antissimétrica
(
![$\delta_{[12]}\phi=-\delta_{[21]}\phi$](img307.png) )
com
)
com
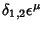 e
e
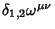 que
seja um escalar. Então,
que
seja um escalar. Então,
Daí se tira imediatamente que
![\begin{displaymath}[P^\lambda,P^\omega]=0 \;.
\end{displaymath}](img352.png) |
(173) |
Comparando os termos que contêm produtos
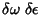 , vê-se que
, vê-se que
e
Antissimetrizando o primeiro termo em relação a 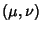 ,
tem-se
,
tem-se
de onde se tira, finalmente,
![\begin{displaymath}
\frac{1}{i}[P^\lambda,J^{\mu \nu}]=P^\nu g^{\mu \lambda}-P^\mu g^{\nu
\lambda}
\end{displaymath}](img360.png) |
(177) |
Casos importantes são:
De maneira análoga se obtém
![\begin{displaymath}
\frac{1}{i}\left[J_{\mu \nu},J_{\kappa \lambda}\right]=g_{\m...
...a}+g_{\nu
\lambda}J_{\mu \kappa}-g_{\mu \lambda}J_{\nu \kappa}
\end{displaymath}](img363.png) |
(180) |



Next: About this document ...
Up: Simetrias fundamentais
Previous: A questão do termo
Henrique Fleming
2001-12-26