


Next: A questão do termo
Up: Simetrias fundamentais
Previous: Transformações unitárias
As transfromações infinitesimais de galileu são
transformações de coordenadas
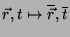 , tais que:
, tais que:
e
 |
(89) |
totalizando 10 parâmetros: 3 vetores (
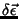 ,
,
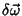 e
e  ) e um escalar (
) e um escalar (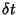 ).
Vamos comparar as aplicações, nas duas ordens, das
transformações
).
Vamos comparar as aplicações, nas duas ordens, das
transformações
ou seja, vamos calcular as seqüências de transfromações
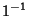 ,
,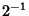 ,
,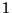 ,
,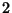 :
:
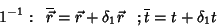 |
(92) |
No que se segue usaremos uma modificação da notação: em lugar de
usaremos 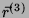 . Assim,
. Assim, 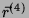 aparecerá também em lugar de
aparecerá também em lugar de
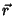 com quatro tracinhos em cima. O mesmo para
com quatro tracinhos em cima. O mesmo para 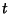 .
.
Definindo
![\begin{displaymath}
\delta_{\left[12\right]}=\delta_2\delta_1-\delta_1\delta_2
\end{displaymath}](img215.png) |
(98) |
temos
![\begin{displaymath}
\delta_{\left[12\right]}\vec{r}=\delta_{\left[12\right]}\vec...
...\vec{\omega})\times\vec{r}
+(\delta_{\left[12\right]}\vec{v})t
\end{displaymath}](img216.png) |
(99) |
Como
o que dá, finalmente,
![\begin{displaymath}
\delta_{\left[12\right]}\vec{\epsilon}=\delta_1\vec{\omega}\...
...c{\epsilon}+\delta_1\vec{v}\delta_2t
-\delta_2\vec{v}\delta_1t
\end{displaymath}](img228.png) |
(103) |
![\begin{displaymath}
\delta_{\left[12\right]}\vec{\omega}=\delta_1\vec{\omega}\times\delta_2\vec{\omega}
\end{displaymath}](img229.png) |
(104) |
![\begin{displaymath}
\delta_{\left[12\right]}\vec{v}=\delta_1\vec{\omega}\times\delta_2\vec{v}-\delta_2\vec{\omega}
\times\delta_1\vec{v}
\end{displaymath}](img230.png) |
(105) |
A transformação unitária infinitesimal que age sobre os estados,
é dada por
![\begin{displaymath}
G=\left[\delta\vec{\epsilon}.\vec{P}+\delta\vec{\omega}.\vec{J}
+\delta\vec{v}.\vec{N}-\delta t\;H\right]+\delta\phi \vec{1}
\end{displaymath}](img232.png) |
(106) |
Os geradores 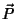 e
e 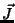 são denominados momento linear e momento angular;
são denominados momento linear e momento angular;
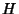 é o operador hamiltomiano; os geradores de variações infinitesimais de velocidades serão
chamados de ``boosts''.
é o operador hamiltomiano; os geradores de variações infinitesimais de velocidades serão
chamados de ``boosts''.
A determinação das constantes de estrutura,e, portanto, das relações de comutação, segue a
estratégia que vamos expor agora.
Pondo
e, lembrando que
![\begin{displaymath}
G_{\left[12\right]}=\frac{1}{i}\left[G_1,G_2\right]
\end{displaymath}](img242.png) |
(110) |
obtém-se:
![\begin{displaymath}
\left[\delta_1\lambda_a G_a,\delta_2 \lambda_b G_b\right]=i\delta_{\left[12\right]}\lambda_c
G_c
\end{displaymath}](img243.png) |
(111) |
Mas o segundo membro é
![\begin{displaymath}
i\left(\delta_{\left[12\right]}\epsilon_k P_k+\delta_{\left[...
...a_{\left[12\right]}v_k N_k-\delta_{\left[12\right]} t H\right)
\end{displaymath}](img244.png) |
(112) |
de maneira que, comparando os dois membros, deduzem-se as
relações de comutação.
Exemplo:
Não sabemos ainda como determinar
![$\delta_{\left[12\right]}\phi$](img251.png) , por não
existir transformação clássica correspondente. Na seção
seguinte mostraremos como determiná-la. O resultado que se obtém
é:
, por não
existir transformação clássica correspondente. Na seção
seguinte mostraremos como determiná-la. O resultado que se obtém
é:
![\begin{displaymath}
\delta_{\left[12\right]}\phi =
M(\delta_1\vec{\epsilon}.\delta_2\vec{v}-\delta_2\vec{\epsilon}.\delta_1\vec{v})\;.
\end{displaymath}](img252.png) |
(117) |
Com isto, todas as relações de comutação podem ser
escritas. Elas são:
![$\displaystyle \left[J_k,J_l\right]$](img253.png) |
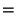 |
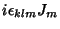 |
(118) |
![$\displaystyle \left[P_k, J_l\right]$](img255.png) |
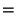 |
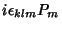 |
(119) |
![$\displaystyle \left[N_k,N_l\right]=0$](img257.png) |
|
|
(120) |
![$\displaystyle \left[P_k,H\right]=0$](img258.png) |
|
|
(121) |
![$\displaystyle \left[N_k,J_l\right]=i\epsilon_{klm}N_m$](img259.png) |
|
|
(122) |
![$\displaystyle \left[P_k,P_l\right]=0$](img260.png) |
|
|
(123) |
![$\displaystyle \left[P_k,N_l\right]=i\delta_{kl}M$](img261.png) |
|
|
(124) |
![$\displaystyle \left[J_k,H\right]=0$](img262.png) |
|
|
(125) |
![$\displaystyle \left[N_k,H\right]=-iP_k$](img263.png) |
|
|
(126) |
Note que
![\begin{displaymath}
G_{[12]}=\frac{1}{i}[G_1,G_2]=\delta_2 G_1=-\delta_1 G_2
\end{displaymath}](img264.png) |
(127) |
pois
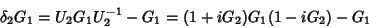 |
(128) |
![\begin{displaymath}
\delta_2G_1=\frac{1}{i}[G_1,G_2]
\end{displaymath}](img266.png) |
(129) |
Usando esta notação, podemos escrever
e, da mesma forma,
![\begin{displaymath}
\delta_{\omega}\vec{P}=\frac{1}{i}[\vec{P},\vec{J}.\delta\vec{\omega}]=\delta\vec{\omega}
\times\vec{P}
\end{displaymath}](img270.png) |
(132) |
![\begin{displaymath}
\delta_{\omega}\vec{N}=\frac{1}{i}[\vec{N},\vec{J}.\delta\vec{\omega}]=\delta\vec{\omega}
\times\vec{N}
\end{displaymath}](img271.png) |
(133) |
que revelam a resposta de um vetor a rotações infinitesimais, e
![\begin{displaymath}
\delta_{\omega} H=\frac{1}{i}[H,\vec{J}.\delta\vec{\omega}]=0
\end{displaymath}](img272.png) |
(134) |
que caracteriza 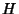 como um escalar sob rotações.
como um escalar sob rotações.
Analogamente, as respostas a translações infinitesimais são
![\begin{displaymath}
\delta_{\epsilon}\vec{J}=\frac{1}{i}[\vec{J},\vec{P}.\delta_{\epsilon}]=
\delta_{\epsilon}\times\vec{P}
\end{displaymath}](img273.png) |
(135) |
![\begin{displaymath}
\delta_{\epsilon}=\frac{1}{i}[\vec{P},\vec{P}.\delta_{\epsilon}]=0
\end{displaymath}](img274.png) |
(136) |
![\begin{displaymath}
\delta_{\epsilon}\vec{N}=\frac{1}{i}[\vec{N},\vec{P}.\delta_{\epsilon}]=-M\delta\vec{\epsilon}
\end{displaymath}](img275.png) |
(137) |
![\begin{displaymath}
\delta_{\epsilon} H=\frac{1}{i}[H,\vec{P}.\delta\vec{\epsilon}]=0
\end{displaymath}](img276.png) |
(138) |
A equação
![\begin{displaymath}
\frac{1}{i}[\vec{J},\vec{P}.\delta\vec{\epsilon}]=\delta\vec{\epsilon}\times \vec{P}
\end{displaymath}](img277.png) |
(139) |
admite a solução
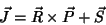 |
(140) |
com
![\begin{displaymath}[R_k,P_l]=i\delta_{kl}
\end{displaymath}](img279.png) |
(141) |
e
![\begin{displaymath}[S_i,P_k]=[S_i,R_k]=0
\end{displaymath}](img280.png) |
(142) |
Para que se mantenham válidas
![$[J_i,J_k]=i\epsilon_{ikl}J_l$](img281.png) , é necessário ainda que
, é necessário ainda que
![\begin{displaymath}[S_i,S_k]=i\epsilon_{ikl}S_l
\end{displaymath}](img282.png) |
(143) |
que podem ser escritas assim:
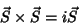 |
(144) |
Finalmente, da resposta de 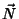 a translações e rtotações, obtém-se
a translações e rtotações, obtém-se
 |
(145) |
Resumindo,
 |
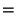 |
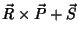 |
(146) |
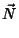 |
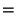 |
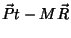 |
(147) |
![$\displaystyle \left[R_i,P_k\right]$](img290.png) |
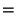 |
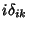 |
(148) |
![$\displaystyle \left[S_i,S_K\right]$](img292.png) |
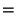 |
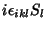 |
(149) |
![$\displaystyle \left[R_i,S_l\right]$](img294.png) |
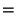 |
![$\displaystyle \left[P_i,S_l\right]=0$](img295.png) |
(150) |
satisfazem automaticamente todas as relações de comutação.
Teorema: os geradores das transformações de relatividade são
constantes do movimento.
Segue diretamente da álgebra.
(i)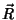 ,
, 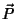 ,
, 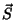 não dependem explicitamente do tempo. Então,
por exemplo,
não dependem explicitamente do tempo. Então,
por exemplo,
![$\frac{d\vec{P}}{dt}=\frac{1}{i}[\vec{P},H]=0$](img298.png) .
.
(ii)
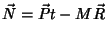 depende explicitamente do tempo. Então,
depende explicitamente do tempo. Então,
![\begin{displaymath}
\frac{d\vec{N}}{dt}=\frac{\partial \vec{N}}{\partial t}+\frac{1}{i}[\vec{N},H]
=\vec{P}-\vec{P}=0
\end{displaymath}](img300.png) |
(151) |
Seja 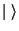 um estado em repouso em relação ao sistema inercial
um estado em repouso em relação ao sistema inercial 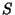 ; seja
; seja
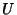 omoperador de transformação infinitesimal ``de relatividade''. Então
omoperador de transformação infinitesimal ``de relatividade''. Então
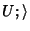 é um estado, e, na verdade, pode ser considerado como o mesmo estado,
visto de um novo sistema de referência
é um estado, e, na verdade, pode ser considerado como o mesmo estado,
visto de um novo sistema de referência  , obtido do primeiro por uma
transformação de relatividade que corresponde a uma escolha fixa dos parâmetros.
A relação entre
, obtido do primeiro por uma
transformação de relatividade que corresponde a uma escolha fixa dos parâmetros.
A relação entre 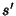 e
e 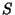 (em termos de parâmetros) não depende do tempo.
Por isso os geradores não podem depender do tempo.
(em termos de parâmetros) não depende do tempo.
Por isso os geradores não podem depender do tempo.
Subsections



Next: A questão do termo
Up: Simetrias fundamentais
Previous: Transformações unitárias
Henrique Fleming
2001-12-26
![]() e
e ![]() são denominados momento linear e momento angular;
são denominados momento linear e momento angular;
![]() é o operador hamiltomiano; os geradores de variações infinitesimais de velocidades serão
chamados de ``boosts''.
é o operador hamiltomiano; os geradores de variações infinitesimais de velocidades serão
chamados de ``boosts''.
![]() ,
, ![]() ,
, ![]() não dependem explicitamente do tempo. Então,
por exemplo,
não dependem explicitamente do tempo. Então,
por exemplo,
![]() .
.
![]() depende explicitamente do tempo. Então,
depende explicitamente do tempo. Então,
![]() um estado em repouso em relação ao sistema inercial
um estado em repouso em relação ao sistema inercial ![]() ; seja
; seja
![]() omoperador de transformação infinitesimal ``de relatividade''. Então
omoperador de transformação infinitesimal ``de relatividade''. Então
![]() é um estado, e, na verdade, pode ser considerado como o mesmo estado,
visto de um novo sistema de referência
é um estado, e, na verdade, pode ser considerado como o mesmo estado,
visto de um novo sistema de referência ![]() , obtido do primeiro por uma
transformação de relatividade que corresponde a uma escolha fixa dos parâmetros.
A relação entre
, obtido do primeiro por uma
transformação de relatividade que corresponde a uma escolha fixa dos parâmetros.
A relação entre ![]() e
e ![]() (em termos de parâmetros) não depende do tempo.
Por isso os geradores não podem depender do tempo.
(em termos de parâmetros) não depende do tempo.
Por isso os geradores não podem depender do tempo.