


Next: A Relatividade de Galileu
Up: Simetrias fundamentais
Previous: Simetrias fundamentais
Na mecânica quântica os estados, situações de máxima
informação, são representados por vetores em um espaço
complexo (bras 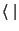 e kets
e kets 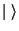 ).
As propriedades físicas são representadas por operadores
lineares hermiteanos sobre este espaço. A liberdade existente na
descrição física corresponde à liberdade de
representação matemática associada a operadores unitários,
).
As propriedades físicas são representadas por operadores
lineares hermiteanos sobre este espaço. A liberdade existente na
descrição física corresponde à liberdade de
representação matemática associada a operadores unitários,
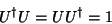 |
(1) |
ou
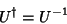 |
(2) |
Quando vetores e operadores são transformados na forma seguinte:
todas as relações numéricas entre vetores e operadores são
conservadas:
Também a relação
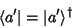 |
(8) |
é conservada:
 |
(9) |
e
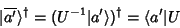 |
(10) |
logo,
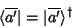 |
(11) |
Finalmente,
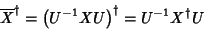 |
(12) |
de maneira que se 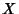 é hermiteano,
é hermiteano, 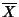 também o é.
também o é.
Um conjunto completo de estados
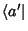 forma uma base do
espaço de estados. Um vetor arbitrário
forma uma base do
espaço de estados. Um vetor arbitrário 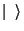 é
representado por suas componentes
é
representado por suas componentes
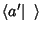 relativas a essa base. A expressão é:
relativas a essa base. A expressão é:
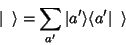 |
(13) |
e a relação
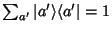 é a relação de completude (entre os físicos,
``completeza'').
é a relação de completude (entre os físicos,
``completeza'').
A partir da base
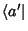 pode-se obter uma outra,
pode-se obter uma outra,
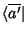 , por uma trnasformação unitária
, por uma trnasformação unitária
 |
(14) |
e as componentes do vetor 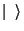 serão
serão
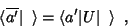 |
(15) |
que podem também ser interpretadas como as componentes, relativas à base
inicial, do vetor 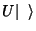 . Analogamente,
. Analogamente,
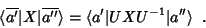 |
(16) |
Suponhamos que sejam realizadas, sobre a base
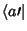 ,
primeiro uma transformação
,
primeiro uma transformação 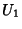 , e a seguir uma
, e a seguir uma  . Do
ponto de vista ``ativo'', o vetor
. Do
ponto de vista ``ativo'', o vetor 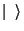 é levado em
é levado em
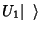 , e este em
, e este em
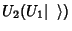 . As
componentes reagem assim:
. As
componentes reagem assim:
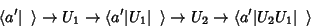 |
(17) |
Esta transformação é produzida, em 1 passo, pelo operador
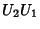 A ordem oposta das operações é efetuada pelo
operador
A ordem oposta das operações é efetuada pelo
operador 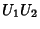 . Seja
. Seja
![$U_{\left[12\right]}$](img40.png) o operador que liga as duas ordens,
ou seja,
o operador que liga as duas ordens,
ou seja,
![\begin{displaymath}
U_{\left[12\right]}U_{1}U_{2}=U_{2}U_{1}
\end{displaymath}](img41.png) |
(18) |
Naturalmente,
![\begin{displaymath}
U_{\left[12\right]}=U_2U_1U_{2}^{-1}U_{1}^{-1}=U_{\left[21\right]}^{-1}
\end{displaymath}](img42.png) |
(19) |
Chama-se transformação unitária infinitesimal uma
transformação da forma
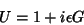 |
(20) |
onde 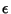 é um número muito pequeno e
é um número muito pequeno e 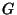 é
hermiteano.Temos
é
hermiteano.Temos
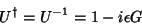 |
(21) |
No que se segue vamos, para aliviar a notação, supor 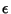 incorporado a
incorporado a 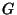 . A transformação infinitesimal será, isto
é, denotada por
. A transformação infinitesimal será, isto
é, denotada por 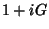 .
.
Suponhamos que  e
e 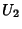 sejam tansformação infinitesimais
unitárias. O operador
sejam tansformação infinitesimais
unitárias. O operador
![$U_{\left[12\right]}$](img40.png) associado a eles é também
unitário. Como a combinação de um número finito de
transformações infinitesimais deve ser uma transformação
infinitesimal, deve existir
associado a eles é também
unitário. Como a combinação de um número finito de
transformações infinitesimais deve ser uma transformação
infinitesimal, deve existir
![$G_{\left[12\right]}$](img50.png) hermiteano, tal que
hermiteano, tal que
![\begin{displaymath}
U_{\left[12\right]}=1+iG_{\left[12\right]}
\end{displaymath}](img51.png) |
(22) |
Qual é a relação entre
![$G_{\left[12\right]}$](img50.png) ,
,  e
e 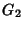 ?
Como
?
Como
![$U_{\left[12\right]}=U_{2}U_{1}U_{2}^{-1}U_{1}^{-1}$](img54.png) , segue que
, segue que
![\begin{displaymath}
U_{\left[12\right]}=(1+iG_{2})(1+iG_{1})(1-iG_{2})(1-iG_{1})
\end{displaymath}](img55.png) |
(23) |
ou
![\begin{displaymath}
U_{\left[12\right]}=1+i^2\left(G_{2}G_{1}-G_{1}G_{2}\right) +
G_{1}G_{1}+G_{2}G_{2}
\end{displaymath}](img57.png) |
(24) |
e, mantendo só os termos lineares,
![\begin{displaymath}
U_{\left[12\right]}=1 + i\left(\frac{1}{i}\left[G_{1},G_{2}\right]\right)=1 + iG_{\left[12\right]}
\end{displaymath}](img58.png) |
(25) |
Note que os termos 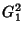 e
e 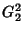 são de segunda ordem, e
são cancelados se se escreve a contribuição completa té
segunda ordem, que é
são de segunda ordem, e
são cancelados se se escreve a contribuição completa té
segunda ordem, que é
![\begin{displaymath}
U_{\left[12\right]}=(1+iG_{2}+\frac{i^2}{2!}G_2G_2)(1+iG_1+\...
..._1)
(1-iG_2+\frac{i^2}{2!}G_2G_2)(1-iG_1+\frac{i^2}{2!}G_1G_1)
\end{displaymath}](img61.png) |
(26) |
Desta maneira, obtemos
![\begin{displaymath}
U_{\left[12\right]}=1+iG_{\left[12\right]}
\end{displaymath}](img51.png) |
(27) |
com
![\begin{displaymath}
G_{\left[12\right]}= -G_{\left[21\right]}=\frac{1}{i}\left[G_1,G_2\right]
\end{displaymath}](img62.png) |
(28) |
que introduz o comutador
![$\left[G_1,G_2\right]$](img63.png) .
.
O efeito de uma transformação infinitesimal unitária sobre um
operador é dado por
![\begin{displaymath}
UXU^{-1}=(1+iG)X(1-iG)=X+iGX-iXG=X+\frac{1}{i}\left[X,G\right]
\end{displaymath}](img64.png) |
(29) |
ou
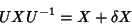 |
(30) |
com
![\begin{displaymath}
\delta X=\frac{1}{i}\left[X,G\right] \;.
\end{displaymath}](img66.png) |
(31) |
Da penúltima equação segue que
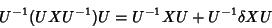 |
(32) |
ou
ou seja,
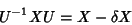 |
(33) |
uponhamos que
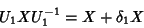 |
(34) |
com
![\begin{displaymath}
\delta_1 X=\frac{1}{i}\left[X,G_1\right]
\end{displaymath}](img71.png) |
(35) |
Queremos calcular
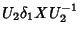 , onde
, onde 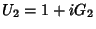 é
outra
transformação infinitesimal unitária. Temos
é
outra
transformação infinitesimal unitária. Temos
=\frac{1}{i}\left[X,G_1\right]+
G_2\left[X,G_1\right]-\left[X,G_1\right]G_2
\end{displaymath}](img74.png) |
(36) |
de maneira que
![\begin{displaymath}
U_2\delta_1X U_2^{-1}=\delta_1X+\frac{1}{i}\left[\frac{i}{i}\left[X,G_1\right],G_2\right]
=\delta_1X +\delta_2\delta_1X
\end{displaymath}](img75.png) |
(37) |
Mais geralmente,
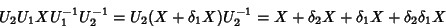 |
(38) |
e, naturalmente,
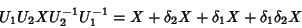 |
(39) |
Finalmente,
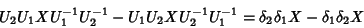 |
(40) |
Notando que
esta última relação pode ser escrita
![\begin{displaymath}
U_{\left[12\right]}U_1U_2XU_2^{-1}U_1^{-1}U_{\left[12\right]}^{-1}-U_1U_2XU_2^{-1}U_1^{-1}
=\delta_{\left[12\right]}X
\end{displaymath}](img83.png) |
(43) |
Obtém-se assim
![\begin{displaymath}
\delta_{\left[12\right]}X=\delta_2\delta_1X-\delta_1\delta_2X
\end{displaymath}](img84.png) |
(44) |
que, em termos de comutadores, é escrita:
![\begin{displaymath}
\left[X,\left[G_2,G_1\right]\right]+\left[G_1,\left[X,G_2\right]\right]+\left[G_2,\left[G_1,X\right]\right]=0
\end{displaymath}](img85.png) |
(45) |
que é a famosa identidade de Jacobi.
Consideremos agora um grupo de transformações unitárias de 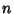 parâmetros
parâmetros 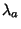 , (
, (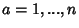 ), abreviados por
), abreviados por  .
Se
.
Se  e
e 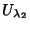 são operadores deste grupo, é
necessário que
são operadores deste grupo, é
necessário que
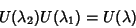 |
(46) |
onde
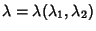 são os parâmetros de
um outro elemento do grupo. Uma transformação infinitesimal do
grupo, com parâmetros
são os parâmetros de
um outro elemento do grupo. Uma transformação infinitesimal do
grupo, com parâmetros
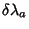 , é construída a
partir de
, é construída a
partir de
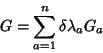 |
(47) |
ou seja,
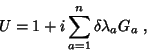 |
(48) |
onde os 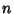 operadores hermiteanos
operadores hermiteanos 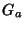 , agora finitos, são
denominados geradores do grupo. Os geradores não são únicos,
dependendo da escolha de parâmetros: transformações lineares
reais e não-singulares dos parâmetros podem ser usadas para passar
a um outro conjunto de geradores.
, agora finitos, são
denominados geradores do grupo. Os geradores não são únicos,
dependendo da escolha de parâmetros: transformações lineares
reais e não-singulares dos parâmetros podem ser usadas para passar
a um outro conjunto de geradores.
Seja
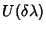 o operador de uma transformação
infinitesimal. Submetendo-a a uma transformação unitária
arbitrária, deve-se obter ainda uma transformação
infinitesimal. Finalmente, devemos ter
o operador de uma transformação
infinitesimal. Submetendo-a a uma transformação unitária
arbitrária, deve-se obter ainda uma transformação
infinitesimal. Finalmente, devemos ter
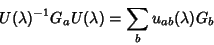 |
(49) |
onde os números
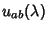 são reais. No espaço dos
parâmetros podemos usar a notação matricial
são reais. No espaço dos
parâmetros podemos usar a notação matricial
 |
(50) |
Associada a esta, temos (aplicando 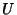 à esquerda,
à esquerda, 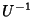 à
direita):
à
direita):
ou, finalmente,
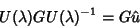 |
(53) |
com
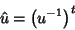 |
(54) |
onde 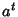 é a transposta da matriz
é a transposta da matriz  .
.
Note-se que, se as 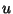 forem unitárias, temos
forem unitárias, temos
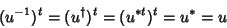 |
(55) |
de maneira que, para 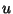 unitárias,
unitárias, 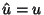 .
.
As matrizes 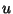 e
e 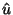 são representações
do grupo unitário a
são representações
do grupo unitário a 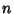 parâmetros
parâmetros 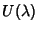 . (Esta particular
representação é denominada representação adjunta).De
fato, a
associação de
. (Esta particular
representação é denominada representação adjunta).De
fato, a
associação de 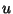 (e
(e 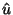 ) a um operador unitário
) a um operador unitário 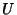 é
linear e preserva a multiplicação, pois
é
linear e preserva a multiplicação, pois
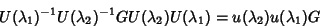 |
(56) |
e
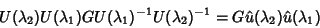 |
(57) |
Como a matriz 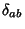 está associada ao operador
está associada ao operador 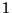 , podemos
escrever
, podemos
escrever
Comop
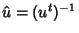 , segue que
, segue que
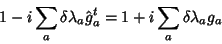 |
(60) |
ou
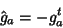 |
(61) |
Se as matrizes 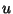 ,
, 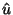 forem unitárias,
forem unitárias,  .
.
Como se transforma 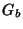 por uma transformação infinitesimal
unitária?
por uma transformação infinitesimal
unitária?
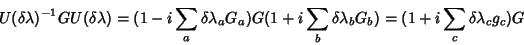 |
(62) |
dando
![\begin{displaymath}
i\delta\lambda_b\left[G,G_b\right]=i\delta\lambda_bg_bG
\end{displaymath}](img130.png) |
(63) |
ou
![\begin{displaymath}
\left[G,G_b\right]=g_bG=-G\hat{g}_b
\end{displaymath}](img131.png) |
(64) |
Introduzindo a notação
 |
(65) |
temos
![\begin{displaymath}
\left[G_a,G_b\right]=\sum_c(g_b)_{ac}G_c=\sum_cg_{abc}G_c
\end{displaymath}](img133.png) |
(66) |
e daí se vê que
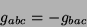 |
(67) |
Note-se que, no caso de 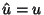 , temos
, temos
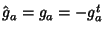 ,
ou seja,
,
ou seja, 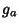 é antissimétrica. Logo, neste caso, adicionalmente,
é antissimétrica. Logo, neste caso, adicionalmente,
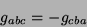 |
(68) |
e as ``constantes de estrutura'' são totalmente antissimétricas.
Como decorrência da correspondência (que preserva a
multiplicação) entre 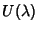 e
e 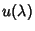 (e
(e
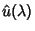 ), as matrizes
), as matrizes 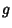 e
e 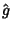 satisfazem as
relações de comutação
satisfazem as
relações de comutação
![\begin{displaymath}
\left[g_a,g_b\right] = \sum_c g_{abc} g_c
\end{displaymath}](img142.png) |
(69) |
e
![\begin{displaymath}
\left[\hat{g}_a,\hat{g}_b\right] = \sum_c g_{abc} \hat{g}_c
\end{displaymath}](img143.png) |
(70) |
De fato, para o caso das 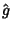 , temos
, temos
![\begin{displaymath}
U_2U_1GU_1^{-1}U_2^{-1}-U_1U_2GU_2^{-1}U_1^{-1}=
G\left(\hat...
...\hat{u}(\lambda_2)\right)=-\left[G,\left[G_1,G_2\right]\right]
\end{displaymath}](img144.png) |
(71) |
Mas,
Por outro lado,
Então
![\begin{displaymath}
-G\sum_{a,b}\delta_1\lambda_b\delta_2\lambda_a\left[\hat{g}_a,\hat{g}_b\right]=g_{abc}\hat{g}_c
\end{displaymath}](img157.png) |
(74) |
e
![\begin{displaymath}
\left[\hat{g}_a,\hat{g}_b\right]=g_{abc}\hat{g}_c
\end{displaymath}](img158.png) |
(75) |
Quod erat demonstrandum.
Essas relações, e suas parentes próximas
![\begin{displaymath}
\left[g_a,g_b\right] = \sum_c g_{abc} g_c
\end{displaymath}](img142.png) |
(76) |
podem ser escritas, por extenso, assim:
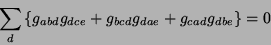 |
(77) |
Uma outra forma, abreviada, é
![\begin{displaymath}
\left[\left[G_a,G_b\right],G_c\right]+\left[\left[G_b,G_c\right],G_a\right]+\left[\left[G_c,G_a\right],G_b\right]=0
\end{displaymath}](img160.png) |
(78) |
que é a identidade de Jacobi.
Vamos introduzir agora um procedimento eficiente para determinar as
constantes de estrutura de um grupo unitário definido a partir de
suas propriedades geométricas.
Pondo
e usando a relação básica
![\begin{displaymath}
U_{\left[12\right]}=U_2U_1U_2^{-1}U_1^{-1}
\end{displaymath}](img167.png) |
(82) |
temos
Assim,
![\begin{displaymath}
i\sum_{c}\delta_{\left[12\right]}\lambda_c G_c=i\sum_{b,a,c}\delta_2
\lambda_b \delta_1\lambda_a \frac{1}{i}g_{abc}G_c
\end{displaymath}](img176.png) |
(85) |
e, finalmente,
![\begin{displaymath}
\delta_{\left[12\right]}\lambda_c=\sum_{a,b}\delta_1\lambda_a \delta_2 \lambda_b
(\frac{1}{i})g_{abc}
\end{displaymath}](img177.png) |
(86) |



Next: A Relatividade de Galileu
Up: Simetrias fundamentais
Previous: Simetrias fundamentais
Henrique Fleming
2001-12-26
![]() forma uma base do
espaço de estados. Um vetor arbitrário
forma uma base do
espaço de estados. Um vetor arbitrário ![]() é
representado por suas componentes
é
representado por suas componentes
![]() relativas a essa base. A expressão é:
relativas a essa base. A expressão é:
![]() pode-se obter uma outra,
pode-se obter uma outra,
![]() , por uma trnasformação unitária
, por uma trnasformação unitária
![]() ,
primeiro uma transformação
,
primeiro uma transformação ![]() , e a seguir uma
, e a seguir uma ![]() . Do
ponto de vista ``ativo'', o vetor
. Do
ponto de vista ``ativo'', o vetor ![]() é levado em
é levado em
![]() , e este em
, e este em
![]() . As
componentes reagem assim:
. As
componentes reagem assim:
![]() e
e ![]() sejam tansformação infinitesimais
unitárias. O operador
sejam tansformação infinitesimais
unitárias. O operador
![]() associado a eles é também
unitário. Como a combinação de um número finito de
transformações infinitesimais deve ser uma transformação
infinitesimal, deve existir
associado a eles é também
unitário. Como a combinação de um número finito de
transformações infinitesimais deve ser uma transformação
infinitesimal, deve existir
![]() hermiteano, tal que
hermiteano, tal que
![]() e
e ![]() são de segunda ordem, e
são cancelados se se escreve a contribuição completa té
segunda ordem, que é
são de segunda ordem, e
são cancelados se se escreve a contribuição completa té
segunda ordem, que é
![]() parâmetros
parâmetros ![]() , (
, (![]() ), abreviados por
), abreviados por ![]() .
Se
.
Se ![]() e
e ![]() são operadores deste grupo, é
necessário que
são operadores deste grupo, é
necessário que
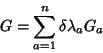
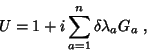
![]() o operador de uma transformação
infinitesimal. Submetendo-a a uma transformação unitária
arbitrária, deve-se obter ainda uma transformação
infinitesimal. Finalmente, devemos ter
o operador de uma transformação
infinitesimal. Submetendo-a a uma transformação unitária
arbitrária, deve-se obter ainda uma transformação
infinitesimal. Finalmente, devemos ter
![]() forem unitárias, temos
forem unitárias, temos
![]() e
e ![]() são representações
do grupo unitário a
são representações
do grupo unitário a ![]() parâmetros
parâmetros ![]() . (Esta particular
representação é denominada representação adjunta).De
fato, a
associação de
. (Esta particular
representação é denominada representação adjunta).De
fato, a
associação de ![]() (e
(e ![]() ) a um operador unitário
) a um operador unitário ![]() é
linear e preserva a multiplicação, pois
é
linear e preserva a multiplicação, pois
![]() está associada ao operador
está associada ao operador ![]() , podemos
escrever
, podemos
escrever
![]() por uma transformação infinitesimal
unitária?
por uma transformação infinitesimal
unitária?
![]() e
e ![]() (e
(e
![]() ), as matrizes
), as matrizes ![]() e
e ![]() satisfazem as
relações de comutação
satisfazem as
relações de comutação

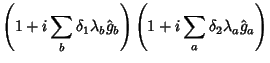
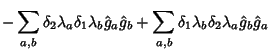
![$\displaystyle +\sum_{a,b}\delta_1\lambda_b\delta_2\lambda_a\left[\hat{g}_a,\hat{g}_b\right]$](img150.png)
![$\displaystyle \left[G,\left[1+i\sum_b\delta_1\lambda_b
G_b,1+i\sum_a\delta_2\lambda_a G_a\right]\right]$](img152.png)
![$\displaystyle \left[G, -\sum_{b,a}\delta_1\lambda_b\delta_2\lambda_a\left[G_b,G_a\right]\right]$](img153.png)
![$\displaystyle -\sum_{b,a}\delta_1\lambda_b\delta_2\lambda_a\left[G,\left[G_b,G_a\right]\right]$](img154.png)
![$\displaystyle -\sum_{b,a}\delta_1\lambda_b\delta_2\lambda_a\left[G,\sum_cg_{abc}G_c\right]$](img155.png)
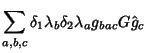
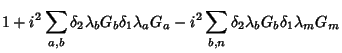
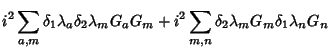
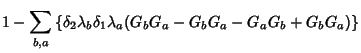
![$\displaystyle 1 + \sum_{b,a}\delta_2\lambda_b \delta_1\lambda_a\left[G_a, G_b\right]$](img175.png)
![\begin{displaymath}
i\sum_{c}\delta_{\left[12\right]}\lambda_c G_c=i\sum_{b,a,c}\delta_2
\lambda_b \delta_1\lambda_a \frac{1}{i}g_{abc}G_c
\end{displaymath}](img176.png)
![\begin{displaymath}
\delta_{\left[12\right]}\lambda_c=\sum_{a,b}\delta_1\lambda_a \delta_2 \lambda_b
(\frac{1}{i})g_{abc}
\end{displaymath}](img177.png)