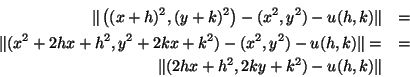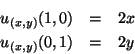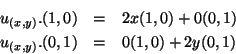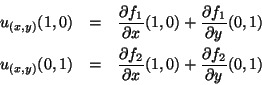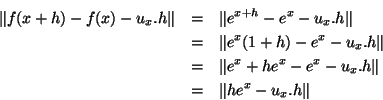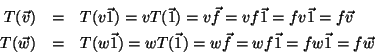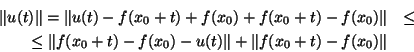Next: Análise em Variedades
Up: Espaço Euclideano
Previous: Formas diferenciais
Nesta seção discutimos funções de  em
em 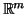 . A
observação fundamentalsobre a função
. A
observação fundamentalsobre a função
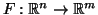 é que ela pode ser completamente descrita por
é que ela pode ser completamente descrita por 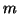 funções de
funções de
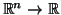 .
.
7.1 Definição Dada uma função
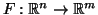 , sejam
, sejam 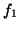 ,...
,... funções reais definidas em
funções reais definidas em 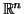 , tais que
, tais que
para todo 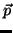 de
de 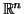 . Essas funções chamam-se
funções coordenadas euclideanas de
. Essas funções chamam-se
funções coordenadas euclideanas de 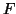 , e é costume
escrever-se:
, e é costume
escrever-se:
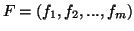 .
A função
.
A função 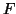 é diferenciável se suas funções
coordenadas o forem. Uma função diferenciável
é diferenciável se suas funções
coordenadas o forem. Uma função diferenciável
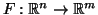 é chamada de mapeamento
de
é chamada de mapeamento
de 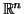 em
em 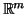 . Note que
. Note que
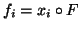 .
.
7.2 Definição Se
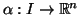 é uma curva em
é uma curva em 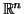 e
e
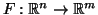 é um mapeamento,
então a função composta
é um mapeamento,
então a função composta
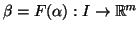 é uma curva em
é uma curva em 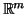 denominada
imagem de
denominada
imagem de 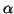 sob
sob 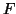 .
.
7.3 Exemplo
(1) Considere o mapeamento
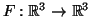 tal
que
tal
que
ou, mais precisamente,
Este mapeamento é muito simples porque é linear. Neste caso é
sabido que 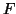 é completamente determinado pelos seus valores em
três pontos linearmente independentes, como, por exemplo,
é completamente determinado pelos seus valores em
três pontos linearmente independentes, como, por exemplo,
(2) O mapeamento
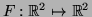 tal que
tal que
onde  e
e 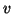 são as funções coordenadas de
são as funções coordenadas de 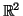 .
Para analisar este mapeamento, vamos examinar o seu efeito sobre a
curva
.
Para analisar este mapeamento, vamos examinar o seu efeito sobre a
curva
Esta curva descreve, em sentido antihorário, um arco de círculo
de raio 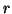 com centro na origem. A curva imagem é
com centro na origem. A curva imagem é
Portanto,
Esta curva descreve dois arcos de círculo, em sentido
antihorário, em torno da origem e de raio 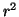 .
Em linhas gerais, o cálculo diferencial aproxima objetos contí
nuos por objetos lineares. Nesta linha, dado um mapeamento
.
Em linhas gerais, o cálculo diferencial aproxima objetos contí
nuos por objetos lineares. Nesta linha, dado um mapeamento
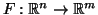 , vamos definir uma aproximação linear para
ele, perto de um ponto
, vamos definir uma aproximação linear para
ele, perto de um ponto
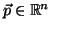 .
É possível atingir todos os pontos de
.
É possível atingir todos os pontos de 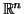 através de retas
através de retas
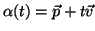 , partindo de
, partindo de 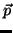 e escolhendo adequadamente
e escolhendo adequadamente
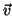 e
e 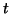 . Da mesma forma
. Da mesma forma 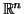 pode ser ``varrido'' pelas imagens de
pode ser ``varrido'' pelas imagens de
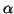 por
por 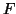 , ou seja,
, ou seja,
começando em 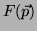 . Vamos aproximar
. Vamos aproximar 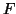 nas vizinhanças de
nas vizinhanças de 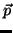 pelo mapeamento
pelo mapeamento 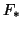 , que leva cada velocidade inicial
, que leva cada velocidade inicial
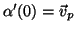 na velocidade inicial
na velocidade inicial
 .
.
7.4 Definição Seja
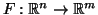 um mapeamento.
Seja
um mapeamento.
Seja 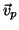 um vetor tangente a
um vetor tangente a 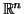 em
em 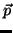 , e denotemos por
, e denotemos por
 a velocidade inicial da curva
a velocidade inicial da curva
A função resultante 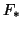 leva vetores tangentes a
leva vetores tangentes a 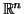 em vetores tangentes
a
em vetores tangentes
a 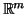 , e é chamada mapeamento tangente de
, e é chamada mapeamento tangente de 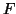 .
.
7.5 Proposição Seja
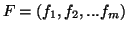 um
mapeamento de
um
mapeamento de 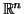 em
em 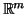 . Se
. Se 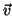 é um vetor tangente
a
é um vetor tangente
a 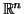 em
em 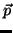 , então
, então
Prova: Vamos tomar 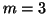 para fixar as idéias. Então
para fixar as idéias. Então
Por definição ,
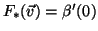 . Para obter
. Para obter
 ,
derivamos, em
,
derivamos, em 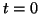 , as funções coordenadas de
, as funções coordenadas de 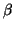 . Mas
. Mas
Logo,
e
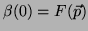 .
.
7.6 Corolário Se
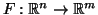 é um mapeamento,
então em cada ponto
é um mapeamento,
então em cada ponto 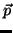 de
de 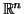 , o mapeamento tangente
, o mapeamento tangente
é uma transformação linear.
Prova: Temos que mostrar que, para 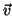 ,
, 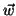 ,
,
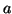 ,
, 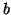 arbitrários,
arbitrários,
De fato, o mapeamento tangente 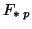 em
em 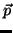 é a transformação
linear que melhor aproxima
é a transformação
linear que melhor aproxima 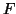 nas vizinhanças de
nas vizinhanças de 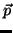 .
.
7.7 Corolário Seja
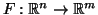 um mapeamento. Se
um mapeamento. Se
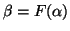 é a imagem da curva
é a imagem da curva 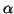 em
em 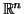 , então
, então
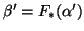 .
.
Prova:
Mas
logo,
Sejam 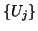 ,
,
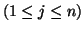 e
e
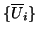 ,
,
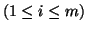 os referenciais naturais de
os referenciais naturais de 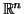 e
e 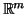 respectivamente.
Então ,
respectivamente.
Então ,
7.8 Corolário Se
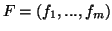 é um mapeamento
de
é um mapeamento
de 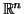 em
em 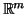 , então
, então
Dem: Imediata, lembrando que
![$U_i[f_j]=\frac{\partial f_j}
{\partial x_i}$](img280.png) .
.
Seja 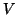 um espaço vetorial, com base
um espaço vetorial, com base  . Seja
. Seja
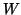 um outro espaço vetorial, com base
um outro espaço vetorial, com base 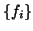 . Seja
. Seja
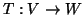 linear. Chama-se elementos de matriz de
linear. Chama-se elementos de matriz de 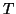 em relação
às bases
em relação
às bases  e
e 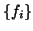 os números
os números 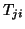 na equação
na equação
Logo, o Corolário 7.8 nos diz que, se
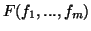 , os elementos
de matriz de
, os elementos
de matriz de 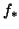 em relação aos referenciais naturais de
em relação aos referenciais naturais de  e
e  são , no ponto
são , no ponto 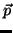 , os números
, os números
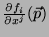 . Ou seja, a matriz que representa a transformação linear
. Ou seja, a matriz que representa a transformação linear 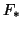 nessas
bases é a matriz jacobiana da função
nessas
bases é a matriz jacobiana da função 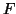 . Isto nos sugere outro nome
para
. Isto nos sugere outro nome
para 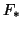 : derivada de
: derivada de 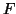 .
.
7.9 Definição Um mapeamento
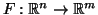 é
regular se, para todo
é
regular se, para todo
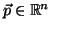 , o mapeamento tangente
, o mapeamento tangente
 for
for  (injetor).1
Como mapeamentos tangentes são lineares, segue diretamente da álgebra linear que as seguintes
condições são equivalentes:
(injetor).1
Como mapeamentos tangentes são lineares, segue diretamente da álgebra linear que as seguintes
condições são equivalentes:
(1)  é injetora.
é injetora.
(2)
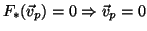
(3) A matriz jacobiana de 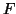 em
em 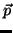 tem posto
tem posto  (que é a dimensão
de
(que é a dimensão
de 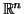 ).
A seguinte propriedade de transformações lineares
).
A seguinte propriedade de transformações lineares
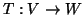 será
útil:se os espaços vetoriais
será
útil:se os espaços vetoriais 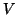 e
e 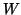 têm a mesma dimensão , então
têm a mesma dimensão , então
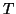 é injetora se e só se ela for sobrejetora.
Um mapeamento que tem um mapeamento inverso é chamado de
difeomorfismo. Lembre-se de que estamos exigindo de um mapeamento que seja
diferenciável. Quando considerarmos aplicações mais gerais, um difeomorfismo
será uma aplicação diferenciável que possui uma inversa também diferenciável.
é injetora se e só se ela for sobrejetora.
Um mapeamento que tem um mapeamento inverso é chamado de
difeomorfismo. Lembre-se de que estamos exigindo de um mapeamento que seja
diferenciável. Quando considerarmos aplicações mais gerais, um difeomorfismo
será uma aplicação diferenciável que possui uma inversa também diferenciável.
7.10 Teorema: Seja
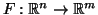 um mapeamento
entre espaços euclideanos de mesma dimensão . Se
um mapeamento
entre espaços euclideanos de mesma dimensão . Se  é injetora
em um ponto
é injetora
em um ponto 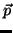 , existe um aberto
, existe um aberto 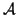 contendo
contendo 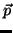 tal que a restrição de
tal que a restrição de 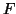 a
a 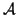 é um difeomorfismo de
é um difeomorfismo de
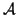 sobre um aberto
sobre um aberto 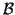 .
Este teorema, de demonstração difícil, é chamado de teorema
da função inversa.
.
Este teorema, de demonstração difícil, é chamado de teorema
da função inversa.
7.11 Definição Funções tangentes.
Seja
 um aberto;
um aberto;  um ponto de
um ponto de  e
e
contínuas em  . Diz-se que
. Diz-se que  e
e  são tangentes em
são tangentes em
 se
se
(1)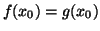
(2)
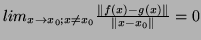
onde 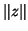 é a norma do vetor
é a norma do vetor  (por exemplo, a norma
euclideana).
O nome se justifica. Tomemos, para simplificar, o caso em que
(por exemplo, a norma
euclideana).
O nome se justifica. Tomemos, para simplificar, o caso em que 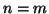 . Então
o limite da definição diz que, se
. Então
o limite da definição diz que, se  e
e  são tangentes em
são tangentes em  , teremos,
próximo a
, teremos,
próximo a  ,
,
e, para que
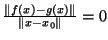 , é preciso que
, é preciso que
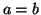 . Ou seja, nas vizinhanças de
. Ou seja, nas vizinhanças de  , as funções tangentes diferem
só a partir da segunda ordem em
, as funções tangentes diferem
só a partir da segunda ordem em  .
.
7.12 Proposição Suponhamos que, dentre as funções tangentes,
em  , à função
, à função  , existam duas funções lineares,
, existam duas funções lineares, 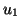 e
e 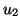 . Isto
é, suponhamos que
. Isto
é, suponhamos que
sejam tangentes a  em
em  . Então,
. Então, 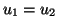 .
.
Prova:
(1)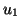 é tangente a
é tangente a 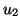 (trivial).
(trivial).
(2) Temos, então ,
Introduzo 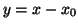 e
e 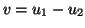 . Então ,
. Então ,
Isto quer dizer que, para qualquer  , existe
, existe 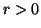 tal que,
se
tal que,
se 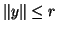 ,
,
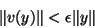 |
(4) |
Considere a seguinte escolha de 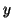 :
:
onde 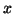 é um vetor não -nulo qualquer. Temos
é um vetor não -nulo qualquer. Temos
e a Eq.(4) vale. Logo,
ou ainda
para 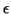 arbitrário e para todo
arbitrário e para todo 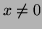 . Para
. Para 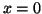 , temos
, temos
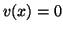 . Para
. Para 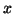 não -nulo, a desigualdade de cima exige
não -nulo, a desigualdade de cima exige 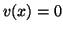 .2 Logo,
.2 Logo,
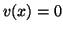 para todo
para todo 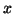 . Segue que
. Segue que 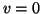 , ou,
, ou, 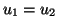 . Em conseqüência a aplicação
linear tangente a uma função contínua em
. Em conseqüência a aplicação
linear tangente a uma função contínua em  , se existir, é única.
, se existir, é única.
7.14 Definição Dizemos que uma aplicação contínua  de
de
 em
em 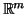 é diferenciável no ponto
é diferenciável no ponto 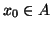 se existir
uma aplicação linear
se existir
uma aplicação linear  de
de
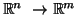 tal que
tal que
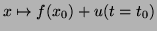 seja tangente a
seja tangente a  em
em  . Acabamos de ver que esse
mapeamento, quando existe, é único.
. Acabamos de ver que esse
mapeamento, quando existe, é único.  é denominado derivada
de
é denominado derivada
de  no ponto
no ponto  , e é denotado por
, e é denotado por 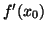 ou
ou 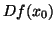 .
.
Exemplos:
1.A aplicação
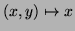 , de
, de
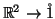 é diferenciável.
Por que? Qual é a sua diferencial?
é diferenciável.
Por que? Qual é a sua diferencial?
A função pode ser escrita  . Ela é linear, pois
. Ela é linear, pois
Como  é linear, ela coincide com a derivada. Então,
é linear, ela coincide com a derivada. Então, 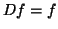 .
.
2.
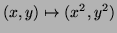 . Determinar a diferencial.
. Determinar a diferencial.
Para ser mais explícito, vou denotar  por
por 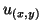 . Considere a
aplicação
. Considere a
aplicação
Então temos
Para que 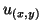 seja a derivada de
seja a derivada de  em
em 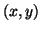 devemos ter
devemos ter
ou seja, que
nolimite em que
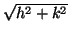 é suficientemente pequeno. Isto é claramente
possível, pois, para
é suficientemente pequeno. Isto é claramente
possível, pois, para 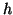 e
e 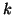 suficientemente pequenos,
suficientemente pequenos,
Resta verificar, o que é muito simples e pode ser feito pelo leitor, que
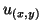 é linear.
Uma vez que
é linear.
Uma vez que
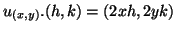 é linear, podemos calcular seus
elementos de matriz. Estes são obtidos aplicando
é linear, podemos calcular seus
elementos de matriz. Estes são obtidos aplicando 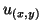 aos
vetores de base de
aos
vetores de base de  :
:
Note-se que
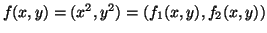 , logo,
, logo,
The partial derivatives of 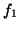 and
and  are given by
are given by
Como podemos escrever
segue, usando os valores das derivadas parciais, que
de onde fica claro que as derivadas parciais são os elementos de
matriz
de 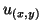 .
.
3.
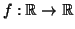 , dada por
, dada por

Para que isto se anule devemos ter
ou seja, a derivada de 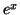 é a função linear
é a função linear
Normalmente dizemos que a derivada da função  no ponto
no ponto
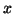 é o número
é o número 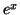 . Isto não é inconsistente. De fato, no
espaço
vetorial
. Isto não é inconsistente. De fato, no
espaço
vetorial 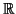 , de uma dimensão, seja
, de uma dimensão, seja  o vetor da base
natural, e
o vetor da base
natural, e 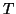 uma aplicação linear qualquer. Seja
uma aplicação linear qualquer. Seja
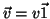 um vetor de
um vetor de 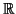 . Temos
. Temos
ou seja, uma aplicação linear
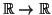 consiste sempre em multiplicar o vetor sobre o qual ela atua por um
número, característico da aplicação, podendo-se então
identificar cada aplicação linear com um número. Na análise
clássica chama-se a esse número de derivada.
consiste sempre em multiplicar o vetor sobre o qual ela atua por um
número, característico da aplicação, podendo-se então
identificar cada aplicação linear com um número. Na análise
clássica chama-se a esse número de derivada.
7.15 Continuidade de uma aplicação linear
Sejam 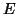 e
e 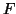 espaços vetoriais com normas definidas e
espaços vetoriais com normas definidas e  uma
aplicação linear de
uma
aplicação linear de 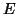 em
em 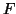 . Afim de que
. Afim de que  seja contínua, é necessário
e suficiente que exista
seja contínua, é necessário
e suficiente que exista 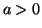 tal que, para todo
tal que, para todo  ,
,
Dem;Elon Lages Lima, Análise Matemática II
7.16 Teorema Se a aplicação contínua  de
de
 em
em 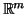 é diferenciável no ponto
é diferenciável no ponto 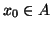 , a derivada
, a derivada 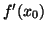 é uma aplicação linear
contínua de
é uma aplicação linear
contínua de
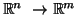 .
.
Dem:A continuidade de  significa que, dado
significa que, dado  , existe
, existe
![$r\in [0,1]$](img376.png) tal que
tal que
A diferenciabilidade em  exige que, nas mesmas condições,
exige que, nas mesmas condições,
Ora,
logo,
e, tomando o máximo 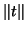 ,
,
Conseqüentemente,
Tomando
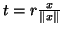 , com
, com 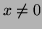 qualquer, temos
qualquer, temos
 . Logo,
. Logo,
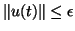 . Mas
. Mas
Logo,
para todo 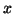 . A função
. A função  é, então, contínua.
é, então, contínua.
7.17 Teorema A regra da cadeia.
Sejam 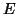 ,
,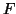 ,
,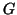 três espaços vetoriais normados,
três espaços vetoriais normados,  uma vizinhança aberta de
uma vizinhança aberta de 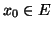 ,
,  uma aplicação contínua de
uma aplicação contínua de  em
em 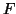 ,
, 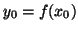 ,
, 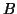 uma vizinhança aberta de
uma vizinhança aberta de  em
em 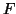 ,
,  uma
aplicação contínua de
uma
aplicação contínua de 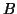 em
em 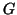 . Então, se
. Então, se  é diferenciável em
é diferenciável em
 e
e  é diferenciável em
é diferenciável em  , a aplicação
, a aplicação 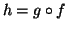 é
diferenciável em
é
diferenciável em  , e se tem
, e se tem
Dem:Too boring inequality juggling! (Dieudonné, Foundations of
Modern Analysis, Parágrafo (8.2.1), pg.151.)



Next: Análise em Variedades
Up: Espaço Euclideano
Previous: Formas diferenciais
Henrique Fleming
2002-10-02

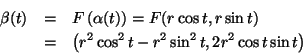
![\begin{eqnarray*}
F_8(a\vec{v}+b\vec{w}) & = &
\left((a\vec{v}+b\vec{w})[f_1],...
...],...,\vec{w}[f_m]\right)\\
& = & aF_*(\vec{v})+bF_*(\vec{w})
\end{eqnarray*}](img267.png)
![\begin{eqnarray*}
m & = & 3\\
F & = & F(\alpha)=(f_1(\alpha),f_2(\alpha),f_3(...
...lpha^\prime[f_1],\alpha^\prime[f_2],
\alpha^\prime[f_3]\right)
\end{eqnarray*}](img271.png)
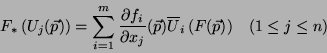
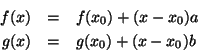
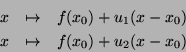
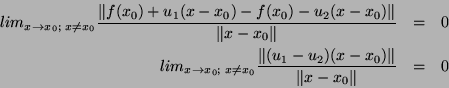
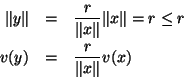
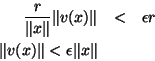
![\begin{eqnarray*}
f[(x,y)+(\overline{x},\overline{y})] & = & f[(x+\overline{x},...
...(x,y)]& = & f[(\lambda x,\lambda y)]=\lambda x = \lambda f(x,y)
\end{eqnarray*}](img341.png)