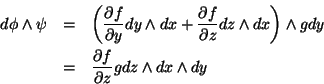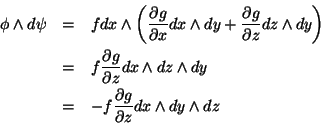Next: Aplicações, ou mapeamentos
Up: Espaço Euclideano
Previous: 1-Formas
As 1-formas são membros de uma família maior, a das
formas diferenciais. Existem 2-formas, 3-formas, etc. De
uma maneira informal, uma forma diferencial é uma soma de termos da
forma 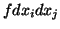 , ou
, ou
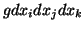 , onde o produto das
diferenciais satisfaz a regra de alternação:
, onde o produto das
diferenciais satisfaz a regra de alternação:
Como conseqüência desta regra, temos
Catálogo:
0-forma: 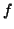 (função diferenciável)
(função diferenciável)
1-forma: 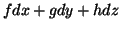
2-forma:
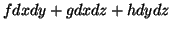
3-forma: 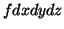 Em
Em 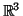 não há outros tipos de formas. Vamos introduzir
operações envolvendo formas. Já sabemos somar 1-formas:
não há outros tipos de formas. Vamos introduzir
operações envolvendo formas. Já sabemos somar 1-formas:
Adições correspondentes existem para 2-formas e 3-formas.
Multiplicação de formas: se faz usando a regra da alternação. Para
ressaltar as propriedades desse produto especial, vamos passar a
denotar o produto 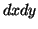 , por exemplo, por
, por exemplo, por 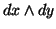 .
.
Exemplo
(1) Sejam
Então,
De uma maneira geral, o produto de duas 1-formas é uma 2-forma.
(2) Sejam 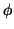 e
e 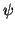 como acima, e
como acima, e 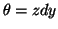 . Então
. Então
Mas
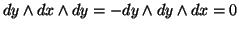 e
e
 Logo,
Logo,
Seja 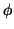 como acima, e seja
como acima, e seja 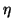 a 2-forma
a 2-forma
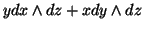 . Temos
. Temos
6.2 Lema Se 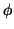 e
e 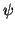 são 1-formas, então
são 1-formas, então
Dem: Trivial.
6.3 Definição Se
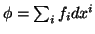 é uma 1-forma em
é uma 1-forma em
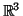 , a derivada exterior de
, a derivada exterior de 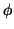 é a 2-forma
é a 2-forma
onde 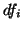 é a diferencial da função
é a diferencial da função 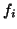 .
.
Seja
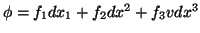 . Então,
. Então,
Mas,
Expandindo e levando em conta as regras do produto exterior, temos
6.4 Teorema Sejam 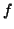 e
e  funções,
funções, 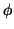 e
e 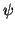 1-formas.
1-formas.
(1)
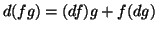
(2)
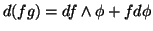
(3)
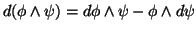
Dem: (1) e (2) são muito simples e ficam como exercícios.
(3) É suficiente provar a fórmula para 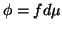 e
e 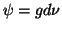 , onde
, onde
 e
e 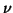 são quaisquer das coordenadas
são quaisquer das coordenadas 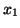 ,
, 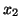 ,
, 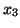 . Por exemplo,
. Por exemplo,
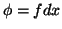 ,
, 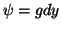 . Então,
. Então,
Mas
o que prova (3).



Next: Aplicações, ou mapeamentos
Up: Espaço Euclideano
Previous: 1-Formas
Henrique Fleming
2002-10-02
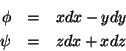
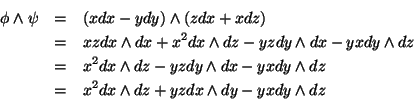

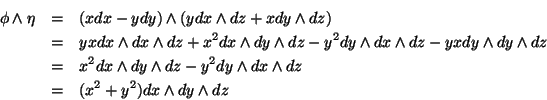
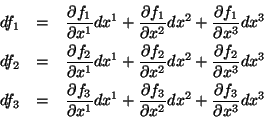
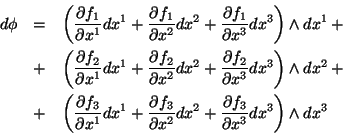
![\begin{eqnarray*}
d(\phi \wedge \psi) & = & d(fg dx\wedge dy) \\
& = & \frac{...
...\frac{\partial g}{\partial z}\right]
dx \wedge dy \wedge dz\\
\end{eqnarray*}](img219.png)