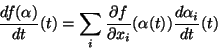Next: 1-Formas
Up: Espaço Euclideano
Previous: Derivadas direcionais
4.1 Definição Uma curva em 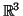 é uma função diferenciável
é uma função diferenciável
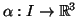 de um intervalo aberto
de um intervalo aberto
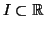 em
em
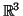 . A função
. A função 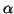 pode ser escrita como
pode ser escrita como
 .
Ser diferenciável quer dizerentão que
.
Ser diferenciável quer dizerentão que
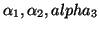 são
diferenciáveis.
são
diferenciáveis.
4.2 Exemplo
1. Reta. É a curva
 definida por
definida por
com  , é a reta passando por
, é a reta passando por 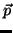 na direção
na direção 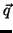 .
2. Hélice. A curva
.
2. Hélice. A curva
 é um
círculo de raio
é um
círculo de raio 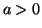 no plano
no plano 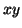 de
de 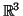 . Uma hélice é obtida
tmando-se a curva
. Uma hélice é obtida
tmando-se a curva
com 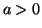 e
e 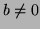 .
.
4.3 Definição Seja
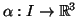 uma curva em
uma curva em 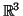 com
com
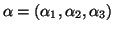 . Para cada
. Para cada 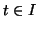 , o vetor velocidade de
, o vetor velocidade de
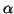 em
em 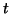 é o vetor tangente
é o vetor tangente
no ponto
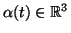 .
.
4.4 Definição Seja
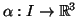 uma
curva. Se
uma
curva. Se
 é uma função diferenciável em um
intervalo aberto
é uma função diferenciável em um
intervalo aberto 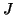 , então a função composta
, então a função composta
é uma curva denominada reparametrização de 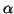 por
por 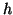 .
.
4.5 Lema Se 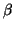 é uma reparametrização de
é uma reparametrização de 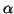 por
por
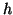 , então
, então
Dem.: Escrevendo
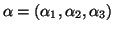 ,
temos
,
temos
Mas
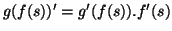 , logo,
, logo,
quod erat demonstrandum.
4.6 LemaSeja 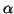 uma curva em
uma curva em 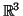 e
seja
e
seja  uma função diferenciável em
uma função diferenciável em 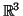 . Então,
. Então,
Prova: como
e como vimos que
temos
Ora,  pode ser escrita
pode ser escrita
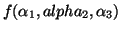 .
Logo,
.
Logo,
Portanto,
Comentário:
![$\alpha^\prime(t)[f]$](img127.png) é a taxa de variação
de
é a taxa de variação
de  ao longo da linha por
ao longo da linha por  , na direção
, na direção
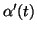 .
O lema mostra que esta taxa é a mesma que a da variação de
.
O lema mostra que esta taxa é a mesma que a da variação de  ao
longo da curva
ao
longo da curva 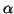 .
.



Next: 1-Formas
Up: Espaço Euclideano
Previous: Derivadas direcionais
Henrique Fleming
2002-10-02