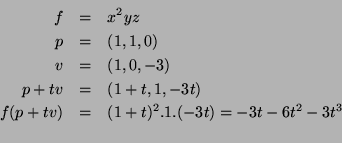Next: Curvas em
Up: Espaço Euclideano
Previous: Vetores Tangentes
Associada a cada vetor tangente
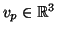 está a reta
está a reta
Seja  uma função diferenciável em
uma função diferenciável em 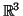 , e considere a função
, e considere a função
que é uma função diferenciável na reta real. É claro que a derivada desta função de 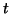 ,
em
,
em 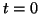 , nos diz como
, nos diz como  varia ao longo da reta que tem a direção de
varia ao longo da reta que tem a direção de 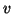 .
.
3.1 Def. Seja
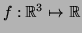 diferenciável, seja
diferenciável, seja 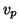 um vetor
tangente a
um vetor
tangente a 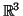 . O número
. O número
é a derivada de  em relação a
em relação a 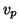 . Outra denominação usada é a de derivada
direcional na direção de
. Outra denominação usada é a de derivada
direcional na direção de 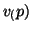 .
.
Exemplo:
e então
Para 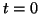 ,
,
O cálculo de ![$v_p[f]$](img60.png) pode ser reduzido ao cálculo das derivadas parciais no
ponto
pode ser reduzido ao cálculo das derivadas parciais no
ponto  , como mostram os lemas a seguir.
, como mostram os lemas a seguir.
3.2 Lema Se
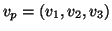 é um vetor tangente a
é um vetor tangente a 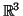 , então
, então
Prova
As principais propriedades dessa derivada direcional são:
3.3 Teorema Sejam
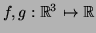 ,
, 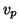 e
e 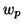 vetores tangentes,
vetores tangentes,
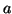 e
e 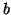 , números. Então,
, números. Então,
de demonstração imediata.
As primeiras duas propriedades podem ser sumarizadas assim: ![$v_p[f]$](img60.png) é linear em
é linear em
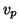 e em
e em  . A terceira é a propriedade de Leibnitz. Todos os tipos de
derivação que vamos encontrar têm essa característica: linearidade e Leibnitz.
Dado um campo vetorial
. A terceira é a propriedade de Leibnitz. Todos os tipos de
derivação que vamos encontrar têm essa característica: linearidade e Leibnitz.
Dado um campo vetorial 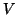 e uma função
e uma função  , podemos falar na função
, podemos falar na função ![$V[f]$](img70.png) . De fato,
em cada ponto
. De fato,
em cada ponto  essa função tem o valor
essa função tem o valor ![$V_p[f]$](img71.png) , ou seja, a derivada de
, ou seja, a derivada de  em
relação ao vetor tangente
em
relação ao vetor tangente 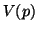 .
Seja
.
Seja 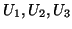 o campo de referenciais naturais em
o campo de referenciais naturais em 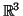 . Lembrando que
. Lembrando que
temos, evidentemente, que
![$U_i[f]=\frac{\partial f}{\partial x^i}$](img79.png) .
Por exemplo:
.
Por exemplo:
3.4 Corolário. Sejam 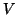 e
e 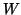 campos vetoriais em
campos vetoriais em 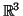 e
e 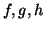 funções reais
funções reais
 .
1.
.
1.
![$(fV+gW)[h]=fV[h]+gW[h]$](img84.png)
2.
![$V[af+bg]=aV[f]+bV[g]$](img85.png)
3.
![$V[fg]=V[f].g+fV[g]$](img86.png)
Demonstração simples. Exemplo:
ou seja;
Para simplificar a notação, nem sempre vamos escrever o ponto de aplicação de um vetro
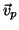 .
.



Next: Curvas em
Up: Espaço Euclideano
Previous: Vetores Tangentes
Henrique Fleming
2002-10-02