


Next: Formas diferenciais
Up: Campos vetoriais: formulação moderna
Previous: Curvas em
Seja
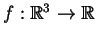 . Elementarmente usa-se
definir a diferencial de
. Elementarmente usa-se
definir a diferencial de 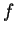 como
sem esclarecer o que esta expressão formal significa. A seguir
daremos um significado preciso à noção de diferencial de uma função.
como
sem esclarecer o que esta expressão formal significa. A seguir
daremos um significado preciso à noção de diferencial de uma função.
5.1 Definição Uma 1-forma em
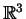 é uma função real
é uma função real 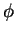 (isto é, a valores reais) sobre o
conjunto dos vetores tangentes a
(isto é, a valores reais) sobre o
conjunto dos vetores tangentes a
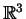 , tal que
, tal que 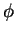 é
linear em cada ponto, isto é,
é
linear em cada ponto, isto é,
para quaisquer números 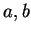 e quaisquer vetores tangentes
e quaisquer vetores tangentes
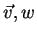 em um ponto arbitrário de
em um ponto arbitrário de
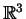 .
Assim, dada
.
Assim, dada 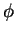 ,
, 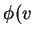 é um número. No ponto
é um número. No ponto
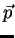 , ponto de aplicação de
, ponto de aplicação de 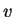 , a função
é linear. Então, em cada ponto
, a função
é linear. Então, em cada ponto 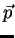 ,
, 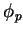 é um elemento
do espaço dual de
é um elemento
do espaço dual de
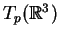 . Neste sentido, a noção de
1-forma é dual à de campo vetorial.
. Neste sentido, a noção de
1-forma é dual à de campo vetorial.
A soma de 1-formas 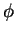 e
e 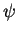 é definida ponto-a-ponto:
é definida ponto-a-ponto:
para todo 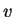 em
em
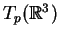 . De modo semelhante, se
. De modo semelhante, se 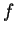 é uma função real em
é uma função real em
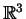 e
e 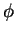 é uma 1-forma,
então a 1-forma
é uma 1-forma,
então a 1-forma 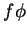 é definida assim:
para todos os vetores tangentes
é definida assim:
para todos os vetores tangentes 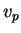 .
.
Daí decorre uma maneira natural para calcular a ação de uma 1-forma
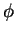 sobre um campo vetorial
sobre um campo vetorial 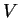 , dando uma função real
, dando uma função real 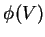 :
:
Pode-se então interpretar também uma 1-forma como uma máquina
que converte campos vetoriais em funções reais. Diz-se que 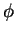 é
diferenciável quando
é
diferenciável quando 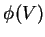 é diferenciável para qualquer
é diferenciável para qualquer 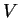 diferenciável. A partir de agora vamos sempre supor que as
1-formas, bem como os campos vetoriais, são diferenciáveis. As
seguintes propriedades da linearidade valem:
diferenciável. A partir de agora vamos sempre supor que as
1-formas, bem como os campos vetoriais, são diferenciáveis. As
seguintes propriedades da linearidade valem:
onde 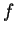 e
e 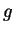 são funções.
são funções.
Usando a noção de derivada direcional vamos introduzir agora uma
maneira muito importante de construir !-formas a partir de funções.
5.2 Definição Seja
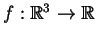 diferenciável. A diferencial
diferenciável. A diferencial 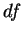 de
de 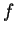 é
uma 1-forma tal que
é
uma 1-forma tal que
para todos os vetores tangentes 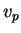 .
.
Comentário: A 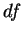 assim definida é efetivamente uma
1-forma, pois é uma função a valores reais sobre os vetores
tangentes e que, pela parte (1) do teorema 3.3, é linear em cada
ponto
assim definida é efetivamente uma
1-forma, pois é uma função a valores reais sobre os vetores
tangentes e que, pela parte (1) do teorema 3.3, é linear em cada
ponto 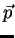 . Note-se que
. Note-se que 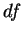 sabe como
sabe como 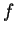 varia em todas as
direções de
varia em todas as
direções de
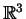 , o que dá uma medida de sua potência.
, o que dá uma medida de sua potência.
5.3 Exemplos 1-formas em
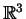 .
.
(1) As diferenciais 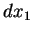 ,
,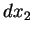 ,
,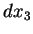 das funções coordenadas
naturais.
das funções coordenadas
naturais.
Assim, o valor de 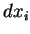 em um vetor tangente arbitrário
em um vetor tangente arbitrário 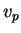 é a i-ésima componente
é a i-ésima componente 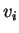 de sua parte vetorial.
de sua parte vetorial.
(2) A 1-forma
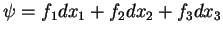
(3) Em particular, tomando como vetores os 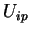 , temos
e, assim,
, temos
e, assim, 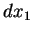 ,
,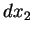 ,
,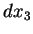 formam a base dual de
formam a base dual de 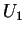 ,
,
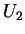 ,
,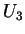 , que é a base natural de
, que é a base natural de
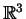 .
.
5.4 Lema Se 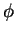 é uma 1-forma em
é uma 1-forma em
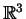 , então
, então
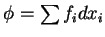 , onde
, onde
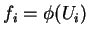 . Essas funções
. Essas funções 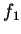 ,
, 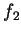 ,
, 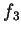 , são chamadas
funções coordenadas euclideanas de
, são chamadas
funções coordenadas euclideanas de 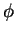 .
.
Dem.: Um vetor tangente genérico pode ser escrito
logo,
onde denotamos
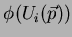 por
por
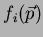 . Mas
logo,
. Mas
logo,
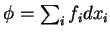 , onde
, onde
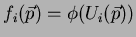 .
.
Este lema mostra que uma 1-forma em
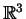 não é senão
uma expressão
não é senão
uma expressão
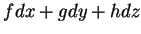 , onde os
, onde os 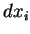 são precisamente
definidos.
são precisamente
definidos.
5.5 Corolário: Seja 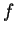 uma função diferenciável
em
uma função diferenciável
em
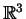 . Então,
. Então,
Dem.:
Ora,
o que demonstra o corolário.



Next: Formas diferenciais
Up: Campos vetoriais: formulação moderna
Previous: Curvas em
Henrique Fleming
2003-08-11
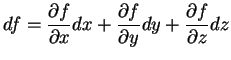
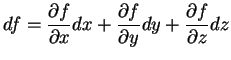
![]() é uma função real
é uma função real ![]() (isto é, a valores reais) sobre o
conjunto dos vetores tangentes a
(isto é, a valores reais) sobre o
conjunto dos vetores tangentes a
![]() , tal que
, tal que ![]() é
linear em cada ponto, isto é,
é
linear em cada ponto, isto é,
![]() e
e ![]() é definida ponto-a-ponto:
é definida ponto-a-ponto:
![]() sobre um campo vetorial
sobre um campo vetorial ![]() , dando uma função real
, dando uma função real ![]() :
:
![]() diferenciável. A diferencial
diferenciável. A diferencial ![]() de
de ![]() é
uma 1-forma tal que
é
uma 1-forma tal que
![]() assim definida é efetivamente uma
1-forma, pois é uma função a valores reais sobre os vetores
tangentes e que, pela parte (1) do teorema 3.3, é linear em cada
ponto
assim definida é efetivamente uma
1-forma, pois é uma função a valores reais sobre os vetores
tangentes e que, pela parte (1) do teorema 3.3, é linear em cada
ponto ![]() . Note-se que
. Note-se que ![]() sabe como
sabe como ![]() varia em todas as
direções de
varia em todas as
direções de
![]() , o que dá uma medida de sua potência.
, o que dá uma medida de sua potência.
![]() .
.
![]() ,
,![]() ,
,![]() das funções coordenadas
naturais.
das funções coordenadas
naturais.
![$\displaystyle dx_i(v_p)=v_p[x_i]=\sum_jv_j\frac{\partial x_i}{\partial
x_j}(\vec{p})=
\sum_j v_j\delta_{ij}=v_i
$](img739.png)
![]() é uma 1-forma em
é uma 1-forma em
![]() , então
, então
![]() , onde
, onde
![]() . Essas funções
. Essas funções ![]() ,
, ![]() ,
, ![]() , são chamadas
funções coordenadas euclideanas de
, são chamadas
funções coordenadas euclideanas de ![]() .
.
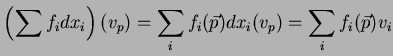
![]() não é senão
uma expressão
não é senão
uma expressão
![]() , onde os
, onde os ![]() são precisamente
definidos.
são precisamente
definidos.
![]() uma função diferenciável
em
uma função diferenciável
em
![]() . Então,
. Então,
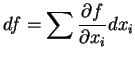
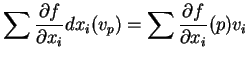
![$\displaystyle df(v_p)=v_p[f]=\sum_i\frac{\partial f}{\partial x_i}
(p)v_i
$](img767.png)