


Next: 1-Formas
Up: Campos vetoriais: formulação moderna
Previous: Derivadas direcionais
4.1 Definição Uma curva em
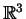 é uma função diferenciável
é uma função diferenciável
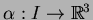 de um intervalo aberto
de um intervalo aberto
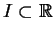 em
em
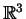 . A função
. A função 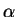 pode ser escrita como
pode ser escrita como
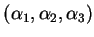 .
Ser diferenciável quer dizerentão que
.
Ser diferenciável quer dizerentão que
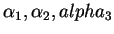 são
diferenciáveis.
são
diferenciáveis.
4.2 Exemplo
1. Reta. É a curva
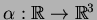 definida por
definida por
com 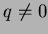 , é a reta passando por
, é a reta passando por 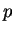 na direção
na direção 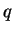 .
.
2. Hélice. A curva
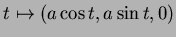 é um
círculo de raio
é um
círculo de raio 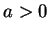 no plano
no plano 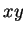 de
de
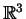 . Uma hélice é obtida
tmando-se a curva
. Uma hélice é obtida
tmando-se a curva
com 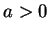 e
e 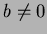 .
.
4.3 Definição Seja
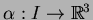 uma curva em
uma curva em
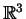 com
com
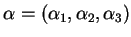 . Para cada
. Para cada 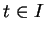 , o vetor velocidade de
, o vetor velocidade de
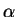 em
em 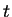 é o vetor tangente
no ponto
é o vetor tangente
no ponto
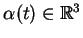 .
.
4.4 Definição Seja
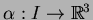 uma
curva. Se
uma
curva. Se
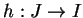 é uma função diferenciável em um
intervalo aberto
é uma função diferenciável em um
intervalo aberto 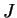 , então a função composta
é uma curva denominada reparametrização de
, então a função composta
é uma curva denominada reparametrização de 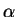 por
por 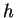 .
.
4.5 Lema Se 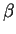 é uma reparametrização de
é uma reparametrização de 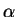 por
por
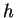 , então
, então
Dem.: Escrevendo
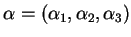 ,
temos
Mas
,
temos
Mas
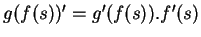 , logo,
quod erat demonstrandum.
, logo,
quod erat demonstrandum.
4.6 LemaSeja 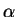 uma curva em
uma curva em
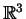 e
seja
e
seja 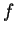 uma função diferenciável em
uma função diferenciável em
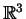 . Então,
. Então,
Prova: como
e como vimos que
temos
Ora, 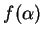 pode ser escrita
pode ser escrita
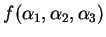 .
Logo,
Portanto,
Comentário:
.
Logo,
Portanto,
Comentário:
![$ \alpha^\prime(t)[f]$](img712.png) é a taxa de variação
de
é a taxa de variação
de 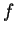 ao longo da linha por
ao longo da linha por 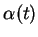 , na direção
, na direção
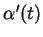 .
O lema mostra que esta taxa é a mesma que a da variação de
.
O lema mostra que esta taxa é a mesma que a da variação de 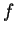 ao
longo da curva
ao
longo da curva 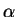 .
.



Next: 1-Formas
Up: Campos vetoriais: formulação moderna
Previous: Derivadas direcionais
Henrique Fleming
2003-08-11
![]() definida por
definida por
![]() é um
círculo de raio
é um
círculo de raio ![]() no plano
no plano ![]() de
de
![]() . Uma hélice é obtida
tmando-se a curva
. Uma hélice é obtida
tmando-se a curva
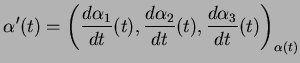
![]() é uma reparametrização de
é uma reparametrização de ![]() por
por
![]() , então
, então
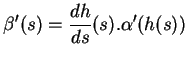
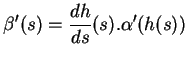
![]() uma curva em
uma curva em
![]() e
seja
e
seja ![]() uma função diferenciável em
uma função diferenciável em
![]() . Então,
. Então,
![$\displaystyle \alpha^\prime(t)[f]=\frac{df(\alpha)}{dt}(t)
$](img704.png)
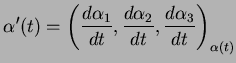
![$\displaystyle \vec{v}_p[f]=\sum v_i\frac{\partial f}{\partial x_i}(\vec{p})
$](img706.png)
![$\displaystyle \alpha^\prime(t)[f]=\alpha^\prime(t)_{\alpha(t)}[f]=
\sum_i\frac{d\alpha_i}{dt}(t)\frac{\partial f}{\partial x_i}
(\alpha(t))
$](img707.png)
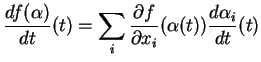
![$\displaystyle \alpha^\prime(t)[f]=\frac{sf(\alpha)}{dt}(t)
$](img711.png)