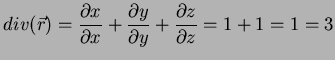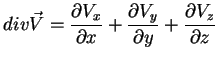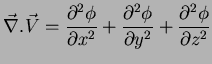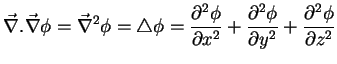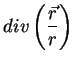Next: Rotações
Up: O operador diferencial
Previous: O operador diferencial
1. Considere o campo vetorial
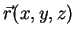 , definido por
, definido por
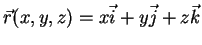 |
(6) |
Podemos calcular o
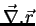 , também denotado por
, também denotado por
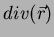 .
.
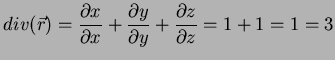 |
(7) |
2. O campo vetorial
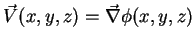 tem o
divergente
tem o
divergente
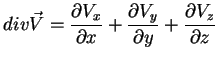 |
(8) |
mas, como
obtemos
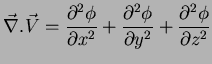 |
(9) |
Esta última expressão é chamada laplaceano de 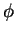 ,
e é, talvez, o operador diferencial mais importante de todos.
Usaremos para ele a notação
,
e é, talvez, o operador diferencial mais importante de todos.
Usaremos para ele a notação
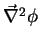 . Encontra-de
também, mas já está um pouco fora de moda, a notação
. Encontra-de
também, mas já está um pouco fora de moda, a notação
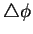 . Assim,
. Assim,
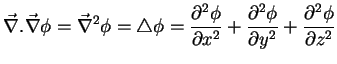 |
(10) |
3.(Exercício) Seja
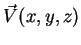 um campo vetorial, e
um campo vetorial, e
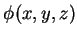 um campo escalar. Mostre que
4.(Exercício) Utilize essa fórmula para calcular
onde
um campo escalar. Mostre que
4.(Exercício) Utilize essa fórmula para calcular
onde
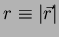 . (Resp:
. (Resp:
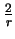 ).
).



Next: Rotações
Up: O operador diferencial
Previous: O operador diferencial
Henrique Fleming
2003-08-11