


Next: Exemplo de grupo de
Up: Grupos de Lie
Previous: Exemplos
Seja  um grupo de Lie e seja
um grupo de Lie e seja 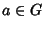 . Considere a aplicação
. Considere a aplicação
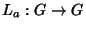 , definida por
, definida por
que é diferenciável. Então existe
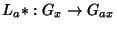 ,
e sua transposta,
,
e sua transposta,
 , bem como suas
extensões homomórficas, denotadas pelos mesmos símbolos.
Note que
, bem como suas
extensões homomórficas, denotadas pelos mesmos símbolos.
Note que  é
é 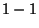 . De fato, sejam
. De fato, sejam
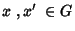 , tais
que
, tais
que
Então, 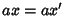 . Como existe
. Como existe 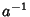 , temos
, temos
QED
Seja 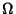 uma forma diferencial sobre
uma forma diferencial sobre  . Diz-se que
. Diz-se que 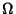 é invariante à esquerda se
é invariante à esquerda se
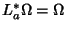 para todo
para todo
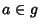 .
.
Proposição: Se 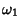 e
e 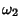 são p-formas invariantes à esquerda, também o serão
são p-formas invariantes à esquerda, também o serão
 e
e
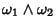 , para quaisquer
, para quaisquer
 e
e  . Além disso,
. Além disso, 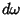 é invariante à esquerda, se
é invariante à esquerda, se
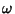 o for.
o for.
Demonstração:
Em outras palavras, o espaço das formas invariantes à esquerda
é uma sub-álgebra da álgebra de todas as formas sobre  , e é
fechada pela operação
, e é
fechada pela operação 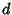 . Chamaremos esta álgebra das formas
invariantes à esquerda, de
. Chamaremos esta álgebra das formas
invariantes à esquerda, de
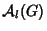 .
.
Seja 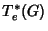 o dual do espaço tangente a
o dual do espaço tangente a  em
em  . Sabemos
que podemos construir, se
. Sabemos
que podemos construir, se 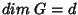 , todas as potências
exteriores
, todas as potências
exteriores
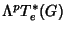 , para
, para 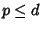 . Denotaremos
por
. Denotaremos
por
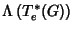 o conjunto de todos os espaços
vetoriais
o conjunto de todos os espaços
vetoriais
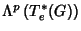 , para
, para
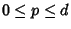 .
.
Teorema Seja  um grupo de Lie e
um grupo de Lie e  o
elemento identidade. O mapeamento
o
elemento identidade. O mapeamento
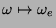 , que
associa a cada p-forma invariante à esquerda sobre
, que
associa a cada p-forma invariante à esquerda sobre  o seu valor
o seu valor
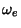 na identidade
na identidade  , é um isomorfismo de
, é um isomorfismo de
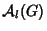 sobre
sobre
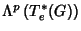 .
.
Dem: o mapeamento é obviamente linear. Vamos mostrar que é 1-1 e
sobrejetor.
1.O mapeamento é injetor (1-1).
Queremos mostrar que, dadas duas p-formas 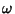 e
e 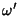 ,
de
,
de
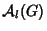 , se
, se
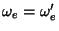 , então
, então
 pata todo
pata todo  , ou seja,
, ou seja,
Pela definição de 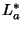 , temos que
, temos que
ou
Como isto é válido para todo 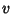 , temos que
, temos que
Tomemos o caso particular
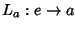 , e, portanto,
, e, portanto,
Então, se 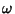 é uma forma em
é uma forma em  e seu valor em
e seu valor em  é
é
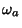 , temos
, temos
e, analogamente,
Mas 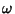 e
e 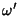 são invariantes à esquerda. Logo,
são invariantes à esquerda. Logo,
Segue que
para qualquer  . Como
. Como 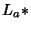 é 1-1, podemos concluir que
é 1-1, podemos concluir que
ou seja,
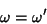 |
(6) |
2.O mapeamento é sobrejetor. Ou seja, dada qualquer forma  em
em
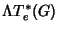 , existe uma forma invariante à esquerda
, existe uma forma invariante à esquerda
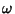 tal que seu valor em
tal que seu valor em  é
é
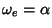 . Seja
. Seja
 . Basta definir
. Basta definir 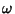 por
por
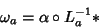 |
(7) |
Então
Em particular, o espaço das 1-formas invariantes à esquerda te
dimensão 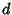 (que é a dimensão de
(que é a dimensão de  ). Seja
). Seja
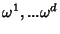 uma base para 1-formas em
uma base para 1-formas em  . Então, como
. Então, como
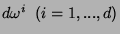 é uma 2-forma invariante à esquerda,
temos
é uma 2-forma invariante à esquerda,
temos
 |
(8) |
Aplicando 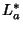 a ambos os mambros, temos
a ambos os mambros, temos
Comparando, temos
 |
(11) |
ou seja, os 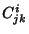 são constantes. Essas constantes são
denominadas constantes de estrutura de
são constantes. Essas constantes são
denominadas constantes de estrutura de  , e as equações
, e as equações
 |
(12) |
são as equações de Maurer-Cartan.
Seja  um campo vetorial sobre
um campo vetorial sobre  . Diz-se que
. Diz-se que  é invariante à esquerda
se
é invariante à esquerda
se
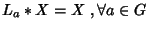 . Se
. Se  e
e  são invariantes à esquerda,
são invariantes à esquerda,
 e
e ![$[X,Y]$](img169.png) também o são (Bishop, pg.139).
também o são (Bishop, pg.139).
Considere o mapeamento dado por 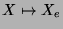 , onde
, onde  é um campo vetorial
invariante à esquerda. Analogamente ao caso de formas, demonstra-se que esse
mapeamento é 1-1 e sobrejetor. Seja então
é um campo vetorial
invariante à esquerda. Analogamente ao caso de formas, demonstra-se que esse
mapeamento é 1-1 e sobrejetor. Seja então
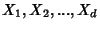 uma base para
campos vetoriais em
uma base para
campos vetoriais em  . Seja
. Seja
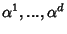 a base de
a base de 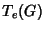 dual da base
dual da base
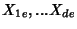 . Sejam ainda
. Sejam ainda
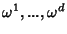 formas invariantes à esquerda
tais que
formas invariantes à esquerda
tais que
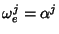 . Então,
. Então,
 |
(13) |
Ora,
![\begin{displaymath}
2d\omega^i(X_j,X_k)=X_j\omega^i(X_k)-X_k\omega^i(X_j)-\omega^i\left([X_j,X_k]\right)
\end{displaymath}](img178.png) |
(14) |
e, como os dois primeiros termos da direita são nulos,
![\begin{displaymath}
2d\omega^i(X_j,X_k)=-\omega^i\left([X_j,X_k]\right)
\end{displaymath}](img179.png) |
(15) |
Por outro lado, das equações de Maurer-Cartan,
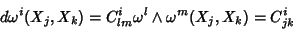 |
(16) |
e, como
![$\omega^i([X_j,X_k])$](img181.png) é a i-ésima componente do campo vetorial
é a i-ésima componente do campo vetorial
![$[X_j,X_k]$](img182.png) na base
na base 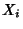 ,
,
![\begin{displaymath}[X_j,X_k]=\omega^i\left([X_j,X_k]\right)=-2C^i_{jk}X_i
\end{displaymath}](img184.png) |
(17) |
Para manter a tradição, definimos novas constantes de estrutura
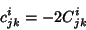 |
(18) |
Então,
![\begin{displaymath}[X_j,X_k]=c^i_{jk}X_i
\end{displaymath}](img186.png) |
(19) |
e
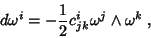 |
(20) |
como se encontra, por exemplo, em Kobayashi, Nomizu, Foundations
of Differential Geometry.



Next: Exemplo de grupo de
Up: Grupos de Lie
Previous: Exemplos
Henrique Fleming
2001-12-26
![]() e
e ![]() são p-formas invariantes à esquerda, também o serão
são p-formas invariantes à esquerda, também o serão
![]() e
e
![]() , para quaisquer
, para quaisquer
![]() e
e ![]() . Além disso,
. Além disso, ![]() é invariante à esquerda, se
é invariante à esquerda, se
![]() o for.
o for.
![]() o dual do espaço tangente a
o dual do espaço tangente a ![]() em
em ![]() . Sabemos
que podemos construir, se
. Sabemos
que podemos construir, se ![]() , todas as potências
exteriores
, todas as potências
exteriores
![]() , para
, para ![]() . Denotaremos
por
. Denotaremos
por
![]() o conjunto de todos os espaços
vetoriais
o conjunto de todos os espaços
vetoriais
![]() , para
, para
![]() .
.
![]() um grupo de Lie e
um grupo de Lie e ![]() o
elemento identidade. O mapeamento
o
elemento identidade. O mapeamento
![]() , que
associa a cada p-forma invariante à esquerda sobre
, que
associa a cada p-forma invariante à esquerda sobre ![]() o seu valor
o seu valor
![]() na identidade
na identidade ![]() , é um isomorfismo de
, é um isomorfismo de
![]() sobre
sobre
![]() .
.
![]() e
e ![]() ,
de
,
de
![]() , se
, se
![]() , então
, então
![]() pata todo
pata todo ![]() , ou seja,
, ou seja,
![]() um campo vetorial sobre
um campo vetorial sobre ![]() . Diz-se que
. Diz-se que ![]() é invariante à esquerda
se
é invariante à esquerda
se
![]() . Se
. Se ![]() e
e ![]() são invariantes à esquerda,
são invariantes à esquerda,
![]() e
e ![]() também o são (Bishop, pg.139).
também o são (Bishop, pg.139).
![]() , onde
, onde ![]() é um campo vetorial
invariante à esquerda. Analogamente ao caso de formas, demonstra-se que esse
mapeamento é 1-1 e sobrejetor. Seja então
é um campo vetorial
invariante à esquerda. Analogamente ao caso de formas, demonstra-se que esse
mapeamento é 1-1 e sobrejetor. Seja então
![]() uma base para
campos vetoriais em
uma base para
campos vetoriais em ![]() . Seja
. Seja
![]() a base de
a base de ![]() dual da base
dual da base
![]() . Sejam ainda
. Sejam ainda
![]() formas invariantes à esquerda
tais que
formas invariantes à esquerda
tais que
![]() . Então,
. Então,