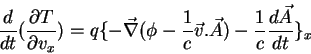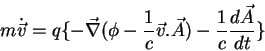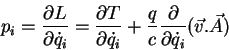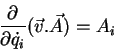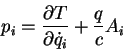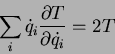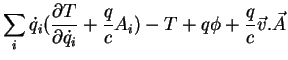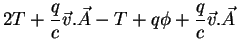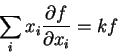Next: About this document ...
Interação Eletromagnética
Formalismo Hamiltoniano
O problema que estudaremos aqui é o seguinte: uma
partícula de massa 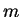 e carga
e carga 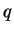 está sob ação de
um campo eletromagnético descrito por
está sob ação de
um campo eletromagnético descrito por 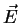 e
e 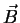 .
Determinar o Hamiltoniano da partícula.
Não fosse pelo campo eletromagnético, o Hamiltoniano seria o de uma
partícula livre,
.
Determinar o Hamiltoniano da partícula.
Não fosse pelo campo eletromagnético, o Hamiltoniano seria o de uma
partícula livre,
A força que age sobre uma partícula de carga 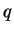 , devida aos campos
elétrico e magnético, é (força de Lorentz):
, devida aos campos
elétrico e magnético, é (força de Lorentz):
Em termos dos potenciais, temos,
Logo,
Como é bem sabido,1
Como
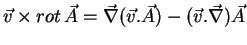 ,
temos
,
temos
ou seja,
![\begin{displaymath}
\vec{F}= q[-\vec{\nabla}(\phi - \frac{1}{c}\vec{v}.\vec{A})
-\frac{1}{c}\frac{d\vec{A}}{dt}] \;.
\end{displaymath}](img20.png) |
(2) |
Seja
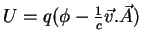 . Vamos mostrar que a
lagrangeana
. Vamos mostrar que a
lagrangeana
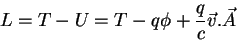 |
(3) |
descreve o movimento de uma partícula sob a ação da força
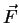 . Aqui, como de costume,
. Aqui, como de costume, 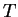 representa a energia cinética.
De fato,
representa a energia cinética.
De fato,
Logo, a equação de Lagrange,
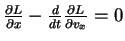 , dá
, dá
de modo que
Mas
de maneira que
Logo,
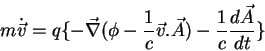 |
(4) |
Conclusão:
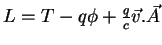 .
Passemos agora à construção do hamiltoniano.
.
Passemos agora à construção do hamiltoniano.
e, então,
Precisamos agora de uma propriedade importante das funções
homogêneas, o teorema de Euler (ver Apêndice):
Vamos usá-lo para calcular o Hamiltoniano 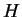 :
:
ou seja,
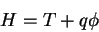 |
(6) |
Ora,
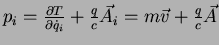 , pois
, pois
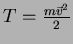 . Logo,
. Logo,
e, finalmente,
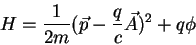 |
(7) |
Em palavras, no Hamiltoniano livre
substituo 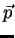 por
por
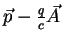 , e adiciono
, e adiciono 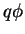 . Esta
é a chamada substituição mínima, ou acoplamento
mínimo. Se o hamiltoniano for mais geral, do tipo
. Esta
é a chamada substituição mínima, ou acoplamento
mínimo. Se o hamiltoniano for mais geral, do tipo
onde 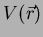 é a energia potencial, a mesma regra vale. Adicione-se
é a energia potencial, a mesma regra vale. Adicione-se
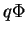 e substitua-se
e substitua-se 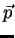 por
por
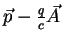 . Se houver
várias partículas, de momentos
. Se houver
várias partículas, de momentos 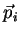 , faça-se a mesma
substituição para cada
, faça-se a mesma
substituição para cada 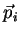 , adicionando-se termos
de energia potencial
, adicionando-se termos
de energia potencial 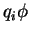 para cada partícula. Essas generalizações
são fáceis de demonstrar, seguindo exatamente o padrão do caso de uma
partícula livre.
para cada partícula. Essas generalizações
são fáceis de demonstrar, seguindo exatamente o padrão do caso de uma
partícula livre.
Apêndice
O teorema de Euler
Uma função
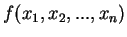 é dita homogênea de grau
é dita homogênea de grau 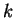 se
se
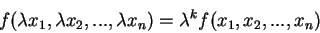 |
(8) |
Por exemplo, 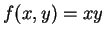 é homogênea de grau 2;
é homogênea de grau 2;
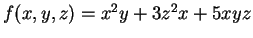 é homogênea de grau 3.
O teorema de Euler diz que, se
é homogênea de grau 3.
O teorema de Euler diz que, se 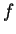 é uma função homogênea de grau
é uma função homogênea de grau
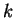 , então
, então
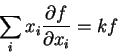 |
(9) |
A demonstração é muito simples. Derive a Eq. 8 em relação
a 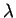 , e depois tome
, e depois tome 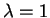 .
.



Next: About this document ...
Henrique Fleming
2002-04-25
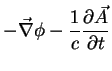
![\begin{displaymath}
\vec{F}=q\{-\vec{\nabla}\phi - \frac{1}{c}[\frac{\partial\vec{A}}
{\partial t}-\vec{v}\times rot\,\vec{A}]\}
\end{displaymath}](img12.png)
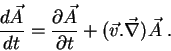
![$\displaystyle q\{-\vec{\nabla}\phi - \frac{1}{c}[\frac{d\vec{A}}{dt}
-(\vec{v}....
...\nabla})\vec{A}-\vec{\nabla}(\vec{v}.\vec{A})
+(\vec{v}.\vec{\nabla})\vec{A}]\}$](img18.png)
![$\displaystyle q\{-\vec{\nabla}\phi - \frac{1}{c}[\frac{d\vec{A}}{dt}-
\vec{\nabla}(\vec{v}.\vec{A})]\}$](img19.png)
![\begin{displaymath}
\vec{F}= q[-\vec{\nabla}(\phi - \frac{1}{c}\vec{v}.\vec{A})
-\frac{1}{c}\frac{d\vec{A}}{dt}] \;.
\end{displaymath}](img20.png)