


Next: Vetores Tangentes
Up: Espaço Euclideano
Previous: Espaço Euclideano
1.1 Def. O espaço euclideano 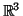 é o conjunto
de todas as triplas ordenadas de números reais. A tripla
é o conjunto
de todas as triplas ordenadas de números reais. A tripla
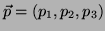 é denominada um ponto
de
é denominada um ponto
de 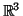
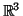 é um espaço vetorial sobre os reais de maneira natural:
se
é um espaço vetorial sobre os reais de maneira natural:
se
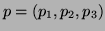 e
e
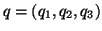 são pontos de
são pontos de 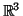 ,
sua soma é o ponto
,
sua soma é o ponto
O múltiplo escalar de um ponto
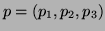 por um
número
por um
número 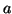 é o ponto
é o ponto
Verifica-se facilmente que essas duas operações satisfazem os axiomas de espaço
vetorial. O ponto 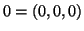 é denominado origem de
é denominado origem de 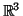
1.2 Def. Sejam 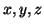 as funções de
as funções de
 tais que, para cada ponto
tais que, para cada ponto
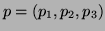 ,
,
Essas funções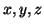 chamam-se funções coordenadas naturais de
chamam-se funções coordenadas naturais de
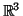 . Também se usa a notação
. Também se usa a notação 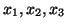 .
.
Vale, então, a identidade
1.3 Def. Uma função real 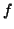 sobre
sobre 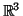 (
(
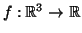 ) é diferenciável (ou de classe
) é diferenciável (ou de classe 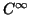 ) se todas as derivadas
pardiais de
) se todas as derivadas
pardiais de 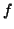 , de todas as ordens, existirem e forem contínuas.
Se
, de todas as ordens, existirem e forem contínuas.
Se 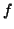 e
e 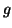 são funções reais diferenciáveis,
são funções reais diferenciáveis, 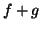 e
e 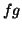 são também
diferenciáveis.
são também
diferenciáveis.
Comentário A diferenciação é uma operação local: para calcular
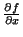 em
em
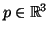 basta saber os valores de
basta saber os valores de 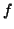 para todos os
para todos os
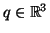 suficientemente próximos de
suficientemente próximos de  . Por isso
a definição acima é excessivamente restritiva. O domínio de
. Por isso
a definição acima é excessivamente restritiva. O domínio de 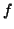 pode ser
um aberto que contenha
pode ser
um aberto que contenha  (e não necessariamente todo o
(e não necessariamente todo o 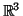 ).
).



Next: Vetores Tangentes
Up: Espaço Euclideano
Previous: Espaço Euclideano
Henrique Fleming
2002-10-02