


Next: About this document ...
Up: Análise em Variedades
Previous: Análise em Variedades
8.1.3 Definição Seja 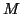 um espaço topológico. Uma carta
(
um espaço topológico. Uma carta
(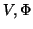 ) é um homeomorfismo
) é um homeomorfismo 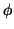 de um aberto
de um aberto 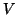 de
de 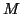 sobre um aberto de
sobre um aberto de
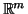 . Duas cartas
. Duas cartas  e
e 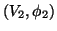 são compatíveis se
são compatíveis se
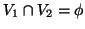 ou, caso contrário, se
ou, caso contrário, se
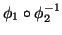 e
e
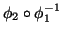 forem aplicações diferenciáveis entre abertos de
forem aplicações diferenciáveis entre abertos de 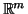
8.1.4 Definição Um atlas é um conjunto de cartas
compatíveis que cobre 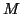 . Dois atlas são compatíveis se todas as suas cartas
são compatíveis.
. Dois atlas são compatíveis se todas as suas cartas
são compatíveis.
8.1.5 Observações
1. No conjunto dos atlas de 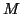 , a relação ``
, a relação ``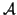 e
e 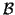 são
compatíveis''é uma relação de equivalência. Então é possível agrupar
os atlas em classes: todos os elementos de uma determinada classe são atlas
equivalentes. Nenhum atlas de uma classe é equivalente a um atlas de outra classe.
são
compatíveis''é uma relação de equivalência. Então é possível agrupar
os atlas em classes: todos os elementos de uma determinada classe são atlas
equivalentes. Nenhum atlas de uma classe é equivalente a um atlas de outra classe.
2.A união de todos os atlas de uma dada classe de equivalência é o
máximo atlas dessa classe. É denominado o atlas
saturado dessa classe. Uma carta compatível com todas as cartas
de um atlas 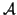 pertence o atlas saturado da classe de equivalência de
pertence o atlas saturado da classe de equivalência de
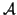 .
.
3. As cartas mapeiam 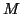 em
em 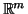 . Diz-se então que
. Diz-se então que 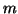 é a
dimensão de
é a
dimensão de 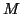 .
.
8.1.6 Definição Uma variedade diferenciável 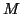 é um
espaço topológico separável, metrizável, com uma classe de
equivalência de atlas, ou, o que é o mesmo, com um atlas saturado.
é um
espaço topológico separável, metrizável, com uma classe de
equivalência de atlas, ou, o que é o mesmo, com um atlas saturado.
8.1.7 Exemplos
1.
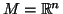
O atlas é formado por uma única carta 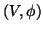 com
com
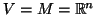
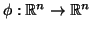 é a identidade,
é a identidade,  .
.
2.A esfera 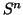 .
.
Seja 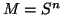 o subconjunto de
o subconjunto de
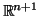 definido por
definido por
não é possível, neste caso, construir um atlas com uma única carta, por
motivos topológicos: 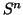 é compacto, e um aberto de
é compacto, e um aberto de 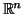 não é compacto. É impossível a existência de um homeomorfismo entre
um compacto e um não-compacto. são necessárias ao menos duas cartas,
não é compacto. É impossível a existência de um homeomorfismo entre
um compacto e um não-compacto. são necessárias ao menos duas cartas,
 e
e 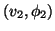 .
.
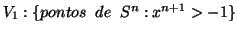 (esfera sem o pólo Sul.)
(esfera sem o pólo Sul.)
 (esfera sem o pólo Norte.)
(esfera sem o pólo Norte.)



Next: About this document ...
Up: Análise em Variedades
Previous: Análise em Variedades
Henrique Fleming
2002-10-02