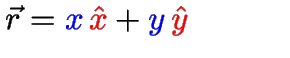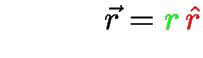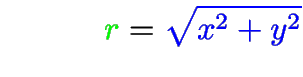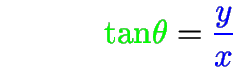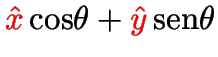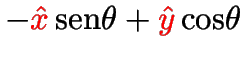Next: Coordenadas Polares
Up: aula1_html
Previous: Livros-texto e provas
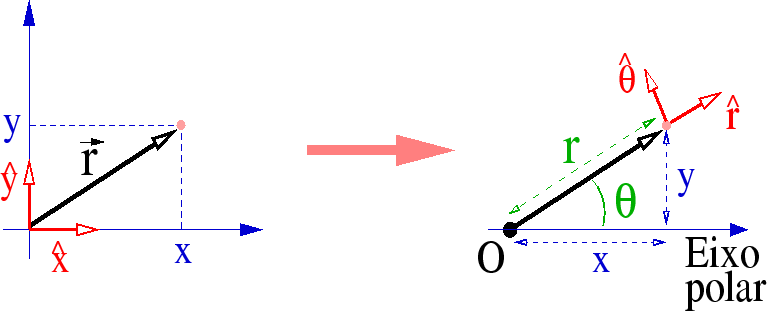
Versores (com chapéu): vetores de norma unitária.
Note que, quando consideramos uma trajetória qualquer,
tanto o raio quanto o ângulo podem ser funções do tempo.
Luis Raul Weber Abramo
2002-08-08